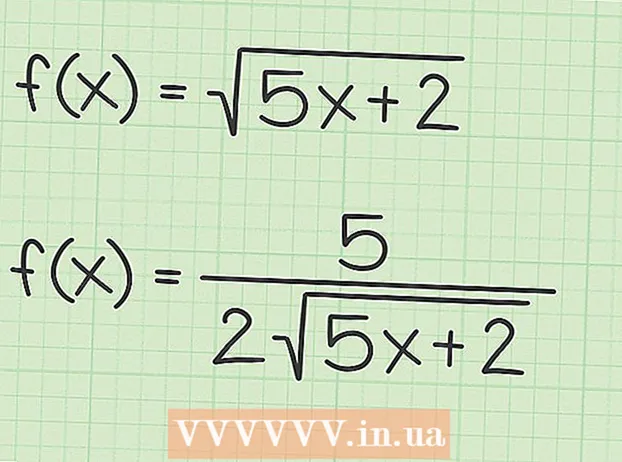
Si heu estudiat matemàtiques a l’escola, sens dubte heu après la regla del poder per determinar la derivada de funcions simples. Tanmateix, quan la funció conté una arrel quadrada o un signe d'arrel quadrada, com ara 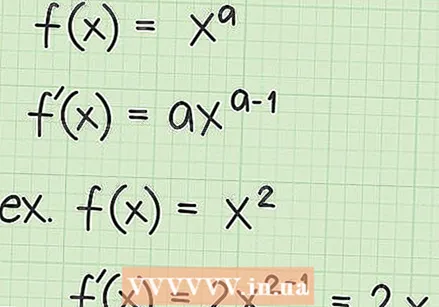${ displaystyle { sqrt {x}}}$Reviseu la regla de potència dels derivats. La primera regla que probablement heu après per trobar derivades és la regla del poder. Aquesta línia diu això per a una variable ${ displaystyle x}$Torneu a escriure l’arrel quadrada com a exponent. Per trobar la derivada d’una funció d’arrel quadrada, recordeu que l’arrel quadrada d’un nombre o variable també es pot escriure com a exponent. El terme sota el signe arrel s’escriu com a base, elevat a la potència de 1/2. El terme també s’utilitza com a exponent de l’arrel quadrada. Mireu els exemples següents:

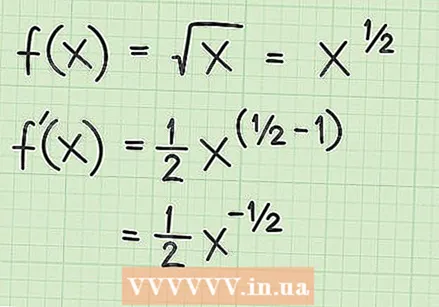• ${ displaystyle { sqrt {x}} = x ^ { frac {1} {2}}}$Apliqueu la regla de potència. Si la funció és l'arrel quadrada més senzilla, 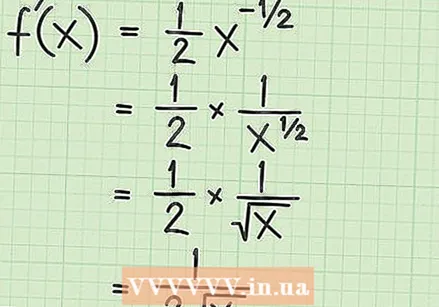${ displaystyle f (x) = { sqrt {x}}}$Simplifiqueu el resultat. En aquesta etapa, heu de saber que un exponent negatiu significa prendre la inversa del que seria el nombre amb l'exponent positiu. L'exponent de 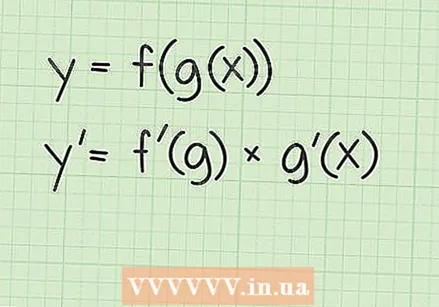${ displaystyle - { frac {1} {2}}}$Reviseu les regles de la cadena. La regla de cadena és una regla per a derivades que utilitzeu quan la funció original combina una funció dins d'una altra funció. La regla de la cadena diu que, per a dues funcions ${ displaystyle f (x)}$Definiu les funcions de la regla de la cadena. L'ús de la regla de la cadena requereix que primer definiu les dues funcions que componen la funció combinada. 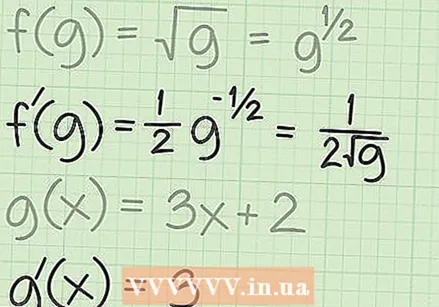Per a les funcions d’arrel quadrada, la funció externa és ${ displaystyle f (g)}$Determina les derivades de les dues funcions. Per aplicar la regla de la cadena a l'arrel quadrada d'una funció, primer heu de trobar la derivada de la funció general d'arrel quadrada:
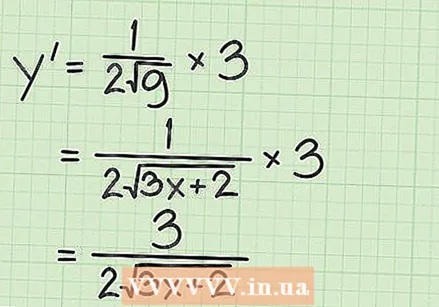  • ${ displaystyle f (g) = { sqrt {g}} = g ^ { frac {1} {2}}}$Combineu les funcions de la regla de la cadena. La regla de la cadena és ${ displaystyle y ^ { prime} = f ^ { prime} (g) * g ^ { prime} (x)}$Determineu les derivades d’una funció arrel mitjançant un mètode ràpid. Quan vulgueu trobar la derivada de l’arrel quadrada d’una variable o una funció, podeu aplicar una regla senzilla: la derivada sempre serà la derivada del nombre situat sota l’arrel quadrada, dividit pel doble de l’arrel quadrada original. Simbòlicament, es pot representar com:
    • Si ${ displaystyle f (x) = { sqrt {u}}}$Cerqueu la derivada del número sota el signe d’arrel quadrada. Es tracta d’un número o funció sota el signe d’arrel quadrada. Per utilitzar aquest mètode ràpid, només busqueu la derivada del número a sota del signe d'arrel quadrada. Penseu en els exemples següents:
      • En la posició ${ displaystyle { sqrt {5x + 2}}}$Escriviu la derivada del número d’arrel quadrada com a numerador d’una fracció. La derivada d’una funció arrel contindrà una fracció. El numerador d’aquesta fracció és la derivada del nombre d’arrel quadrada. Per tant, a les funcions d’exemple anteriors, la primera part de la derivada anirà així:
        • Si 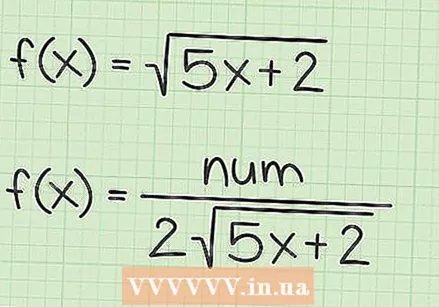${ displaystyle f (x) = { sqrt {5x + 2}}}$Escriviu el denominador com a doble de l’arrel quadrada original. Amb aquest mètode ràpid, el denominador és el doble de la funció d’arrel quadrada original. Per tant, en els tres exemples de funcions anteriors, els denominadors de les derivades són:
          • Si ${ displaystyle f (x) = { sqrt {5x + 2}}}$Combineu el numerador i el denominador per trobar la derivada. Uniu les dues meitats de la fracció i el resultat serà la derivada de la funció original.
            • Si ${ displaystyle f (x) = { sqrt {5x + 2}}}$, que ${ displaystyle f ^ { prime} (x) = { frac {5} {2 { sqrt {5x + 2}}}}}$
            • Si ${ displaystyle f (x) = { sqrt {3x ^ {4}}}}$, que ${ displaystyle f ^ { prime} (x) = { frac {12x ^ {3}} {2 { sqrt {3x ^ {4}}}}}}$
            • Si ${ displaystyle f (x) = { sqrt { sin (x)}}}$, que ${ displaystyle f ^ { prime} (x) = { frac { cos (x)} {2 { sqrt { sin (x)}}}}$