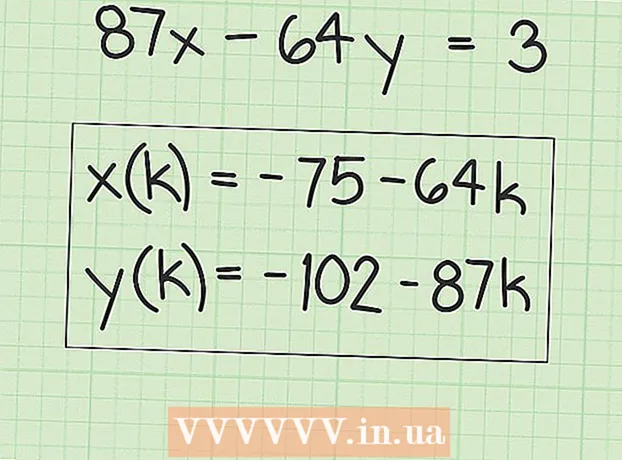
Content

• Passos
• Part 1 de 4: Com escriure una equació
• Part 2 de 4: Com escriure l'algorisme d'Euclides
• Part 3 de 4: Com trobar una solució mitjançant l'algorisme d'Euclides
• Part 4 de 4: trobar altres solucions infinites

Per resoldre una equació diofantina lineal, heu de trobar els valors de les variables "x" i "y", que són enters. Una solució sencera és més complexa de l’habitual i requereix un conjunt específic d’accions. Primer, cal calcular el màxim comú divisor (MCD) dels coeficients i, a continuació, trobar una solució. Un cop heu trobat una solució sencera a una equació lineal, podeu utilitzar un patró senzill per trobar un nombre infinit d'altres solucions.

Passos

Part 1 de 4: Com escriure una equació

1. 1 Escriviu l’equació en forma estàndard. Una equació lineal és una equació en què els exponents de les variables no superen 1. Per resoldre aquesta equació lineal, primer escriviu-la en forma estàndard. La forma estàndard d'una equació lineal té aquest aspecte: ${ displaystyle Ax + By = C}$, on ${ displaystyle A, B}$ i ${ displaystyle C}$ - nombres enters.
   • Si l'equació es dóna en una forma diferent, porteu-la a la forma estàndard mitjançant operacions algebraiques bàsiques. Per exemple, donada l’equació ${ displaystyle 23x + 4y-7x = -3y + 15}$... Doneu termes similars i escriviu l’equació així: ${ displaystyle 16x + 7y = 15}$.
2. 2 Simplifiqueu l’equació (si és possible). Quan escriviu l’equació en forma estàndard, mireu els coeficients ${ displaystyle A, B}$ i ${ displaystyle C}$... Si aquestes probabilitats tenen un GCD, divideix-ne les tres. La solució a una equació tan simplificada també serà la solució a l’equació original.
   • Per exemple, si els tres coeficients són parells, divideix-los per almenys 2. Per exemple:
     • ${ displaystyle 42x + 36y = 48}$ (tots els membres són divisibles per 2)
     • ${ displaystyle 21x + 18y = 24}$ (ara tots els membres són divisibles per 3)
     • ${ displaystyle 7x + 6y = 8}$ (aquesta equació ja no es pot simplificar)
3. 3 Comproveu si l'equació es pot resoldre. En alguns casos, podeu afirmar immediatament que l’equació no té solucions. Si el coeficient "C" no és divisible pel MCD dels coeficients "A" i "B", l'equació no té solucions.
   • Per exemple, si tots dos coeficients ${ displaystyle A}$ i ${ displaystyle B}$ són parells, llavors el coeficient ${ displaystyle C}$ ha de ser parell. Però si ${ displaystyle C}$ estrany, llavors no hi ha solució.
     • L’equació ${ displaystyle 2x + 4y = 21}$ cap solució sencera.
     • L’equació ${ displaystyle 5x + 10y = 17}$ no hi ha solucions senceres ja que el costat esquerre de l'equació és divisible per 5 i el costat dret no.

Part 2 de 4: Com escriure l'algorisme d'Euclides

1. 1 Comprendre l'algorisme d'Euclides. És una sèrie de divisions repetides en què s’utilitza la resta anterior com a divisor següent. L'últim divisor que divideix els nombres integralment és el màxim divisor comú (MCD) dels dos nombres.
   • Per exemple, trobem el MCD dels nombres 272 i 36 mitjançant l'algorisme d'Euclides:
     • ${ displaystyle 272 = 7 * 36 + 20}$ - Divideix el nombre més gran (272) pel menor (36) i presta atenció a la resta (20);
     • ${ displaystyle 36 = 1 * 20 + 16}$ - divideix el divisor anterior (36) per la resta anterior (20). Tingueu en compte el nou residu (16);
     • ${ displaystyle 20 = 1 * 16 + 4}$ - divideix el divisor anterior (20) per la resta anterior (16). Tingueu en compte el nou residu (4);
     • ${ displaystyle 16 = 4 * 4 + 0}$ - Divideix el divisor anterior (16) pel restant anterior (4). Com que la resta és 0, podem dir que 4 és el MCD dels dos números originals 272 i 36.
2. 2 Apliqueu l'algorisme d'Euclides als coeficients "A" i "B". Quan escriviu l'equació lineal en forma estàndard, determineu els coeficients "A" i "B" i, a continuació, apliqueu-los l'algorisme d'Euclides per trobar el GCD. Per exemple, donada una equació lineal ${ displaystyle 87x-64y = 3}$.
   • Aquí teniu l’algorisme d’Euclides per als coeficients A = 87 i B = 64:
     • ${ displaystyle 87 = 1 * 64 + 23}$
     • ${ displaystyle 64 = 2 * 23 + 18}$
     • ${ displaystyle 23 = 1 * 18 + 5}$
     • ${ displaystyle 18 = 3 * 5 + 3}$
     • ${ displaystyle 5 = 1 * 3 + 2}$
     • ${ displaystyle 3 = 1 * 2 + 1}$
     • ${ displaystyle 2 = 2 * 1 + 0}$
3. 3 Trobeu el major factor comú (MCD). Com que l’últim divisor era 1, el MCD 87 i el 64 són 1. Per tant, el 87 i el 64 són nombres primers relatius entre si.
4. 4 Analitzeu el resultat. Quan trobeu els coeficients mcd ${ displaystyle A}$ i ${ displaystyle B}$, compareu-lo amb el coeficient ${ displaystyle C}$ l’equació original. Si ${ displaystyle C}$ divisible per mcd ${ displaystyle A}$ i ${ displaystyle B}$, l'equació té una solució sencera; en cas contrari, l’equació no té solucions.
   • Per exemple, l’equació ${ displaystyle 87x-64y = 3}$ es pot resoldre perquè 3 és divisible per 1 (mcd = 1).
   • Per exemple, suposem GCD = 5. 3 no és divisible per 5, de manera que aquesta equació no té solucions senceres.
   • Com es mostra a continuació, si una equació té una solució sencera, també té un nombre infinit d'altres solucions senceres.

Part 3 de 4: Com trobar una solució mitjançant l'algorisme d'Euclides

1. 1 Numereu els passos per calcular el GCD. Per trobar la solució a una equació lineal, heu d’utilitzar l’algorisme euclidià com a base per al procés de substitució i simplificació.
   • Comenceu numerant els passos per calcular el GCD. El procés de càlcul té aquest aspecte:
     • ${ displaystyle { text {Pas 1}}: 87 = (1 * 64) +23}$
     • ${ displaystyle { text {Pas 2}}: 64 = (2 * 23) +18}$
     • ${ displaystyle { text {Pas 3}}: 23 = (1 * 18) +5}$
     • ${ displaystyle { text {Pas 4}}: 18 = (3 * 5) +3}$
     • ${ displaystyle { text {Pas 5}}: 5 = (1 * 3) +2}$
     • ${ displaystyle { text {Pas 6}}: 3 = (1 * 2) +1}$
     • ${ displaystyle { text {Pas 7}}: 2 = (2 * 1) +0}$
2. 2 Presteu atenció a l’últim pas, on queda una resta. Torneu a escriure l’equació d’aquest pas per aïllar la resta.
   • En el nostre exemple, l’últim pas amb resta és el pas 6. El restant és 1. Torneu a escriure l’equació del pas 6 de la següent manera:
     • ${ displaystyle 1 = 3- (1 * 2)}$
3. 3 Aïlleu la resta del pas anterior. Aquest procés és un pas cap amunt. Cada vegada que aïlleu la resta de l'equació del pas anterior.
   • Aïlleu la resta de l'equació al pas 5:
     • ${ displaystyle 2 = 5- (1 * 3)}$ o bé ${ displaystyle 2 = 5-3}$
4. 4 Substitueix i simplifica. Fixeu-vos que l’equació del pas 6 conté el número 2 i, a l’equació del pas 5, el número 2 està aïllat. Per tant, en lloc de "2" a l'equació del pas 6, substituïu l'expressió del pas 5:
   • ${ displaystyle 1 = 3-2}$ (equació del pas 6)
   • ${ displaystyle 1 = 3- (5-3)}$ (en lloc de 2, s'ha substituït una expressió)
   • ${ displaystyle 1 = 3-5 + 3}$ (claudàtors oberts)
   • ${ displaystyle 1 = 2 (3) -5}$ (simplificat)
5. 5 Repetiu el procés de substitució i simplificació. Repetiu el procés descrit movent-vos a través de l'algorisme euclidià en ordre invers. Cada vegada que reescriviu l'equació del pas anterior i la connectareu a l'última equació que obtingueu.
   • L'últim pas que vam examinar va ser el pas 5. Per tant, aneu al pas 4 i aïlleu la resta de l'equació d'aquest pas:
     • ${ displaystyle 3 = 18- (3 * 5)}$
   • Substitueix aquesta expressió per "3" a la darrera equació:
     • ${ displaystyle 1 = 2 (18-3 * 5) -5}$
     • ${ displaystyle 1 = 2 (18) -6 (5) -5}$
     • ${ displaystyle 1 = 2 (18) -7 (5)}$
6. 6 Continueu amb el procés de substitució i simplificació. Aquest procés es repetirà fins arribar al pas inicial de l'algorisme euclidià. L’objectiu del procés és escriure l’equació amb els coeficients 87 i 64 de l’equació original que es vol resoldre. En el nostre exemple:
   • ${ displaystyle 1 = 2 (18) -7 (5)}$
   • ${ displaystyle 1 = 2 (18) -7 (23-18)}$ (substituït l'expressió del pas 3)
     • ${ displaystyle 1 = 2 (18) -7 (23) +7 (18)}$
     • ${ displaystyle 1 = 9 (18) -7 (23)}$
   • ${ displaystyle 1 = 9 (64-2 * 23) -7 (23)}$ (substituït l'expressió del pas 2)
     • ${ displaystyle 1 = 9 (64) -18 (23) -7 (23)}$
     • ${ displaystyle 1 = 9 (64) -25 (23)}$
   • ${ displaystyle 1 = 9 (64) -25 (87-64)}$ (substituït l'expressió del pas 1)
     • ${ displaystyle 1 = 9 (64) -25 (87) +25 (64)}$
     • ${ displaystyle 1 = 34 (64) -25 (87)}$
7. 7 Torneu a escriure l'equació resultant d'acord amb els coeficients originals. Quan torneu al primer pas de l'algorisme euclidià, veureu que l'equació resultant conté dos coeficients de l'equació original. Torneu a escriure l'equació de manera que l'ordre dels termes coincideixi amb els coeficients de l'equació original.
   • En el nostre exemple, l’equació original ${ displaystyle 87x-64y = 3}$... Per tant, reescriviu l'equació resultant perquè els coeficients es posin en línia.Presteu especial atenció al coeficient "64". A l’equació original, aquest coeficient és negatiu i, en l’algorisme euclidià, és positiu. Per tant, el factor 34 s’ha de fer negatiu. L'equació final s'escriurà així:
     • ${ displaystyle 87 (-25) -64 (-34) = 1}$
8. 8 Apliqueu el multiplicador adequat per trobar una solució. Tingueu en compte que al nostre exemple, GCD = 1, de manera que l'equació final és 1. Però l'equació original (87x-64y) és 3. Per tant, tots els termes de l'equació final s'han de multiplicar per 3 per obtenir la solució:
   • ${ displaystyle 87 (-25 * 3) -64 (-34 * 3) = 1 * 3}$
   • ${ displaystyle 87 (-75) -64 (-102) = 3}$
9. 9 Escriviu la solució sencera a l’equació. Els números que es multipliquen pels coeficients de l’equació original són les solucions d’aquesta equació.
   • Al nostre exemple, escriviu la solució com un parell de coordenades: ${ displaystyle (x, y) = (- 75, -102)}$.

Part 4 de 4: trobar altres solucions infinites

1. 1 Compreneu que hi ha un nombre infinit de solucions. Si una equació lineal té una solució sencera, ha de tenir infinitament moltes solucions enteres. Aquí teniu una prova ràpida (en forma algebraica):
   • ${ displaystyle Ax + By = C}$
   • ${ displaystyle A (x + B) + B (y-A) = C}$ (si afegiu "B" a "x" i resteu "A" de "y", el valor de l'equació original no canviarà)
2. 2 Anoteu els valors originals xy. La plantilla per calcular les properes solucions (infinites) comença amb l’única solució que ja heu trobat.
   • En el nostre exemple, la solució és un parell de coordenades ${ displaystyle (x, y) = (- 75, -102)}$.
3. 3 Afegiu el factor "B" al valor "x". Feu això per trobar el nou valor x.
   • En el nostre exemple, x = -75 i B = -64:
     • ${ displaystyle x = -75 + (- 64) = - 139}$
   • Per tant, el nou valor "x": x = -139.
4. 4 Resteu el factor "A" del valor "y". Perquè el valor de l'equació original no canviï, en afegir un número a "x", heu de restar un altre número de "y".
   • En el nostre exemple, y = -102 i A = 87:
     • ${ displaystyle y = -102-87 = -189}$
   • Per tant, el nou valor de "y": y = -189.
   • El nou parell de coordenades s’escriurà així: ${ displaystyle (x, y) = (- 139, -189)}$.
5. 5 Comproveu la solució. Per verificar que el nou parell de coordenades sigui una solució a l'equació original, connecteu els valors a l'equació.
   • ${ displaystyle 87x-64y = 3}$
   • ${ displaystyle 87 (-139) -64 (-189) = 3}$
   • ${ displaystyle 3 = 3}$
   • Com que es compleix la igualtat, la decisió és correcta.
6. 6 Anoteu expressions per trobar moltes solucions. Els valors "x" igualaran la solució original més qualsevol múltiple del factor "B". Es pot escriure com a expressió següent:
   • x (k) = x + k (B), on "x (k)" és el conjunt de valors "x" i "x" és el (primer) valor original de "x" que heu trobat.
     • En el nostre exemple:
     • ${ displaystyle x (k) = - 75-64k}$
   • y (k) = y-k (A), on y (k) és el conjunt de valors y i y és el valor original (primer) y que heu trobat.
     • En el nostre exemple:
     • ${ displaystyle y (k) = - 102-87k}$