Content

• Passos
• Consells

Si sou un matemàtic o un programador gràfic, probablement haureu de trobar l’angle entre dos vectors donats. En aquest article, wikiHow us mostra com fer-ho.

Passos

Part 1 de 2: Trobeu l'angle entre dos vectors

1. 

   Definició de vectors. Anoteu tota la informació sobre els dos vectors que teniu. Suposem que només teniu els paràmetres especificats de les seves coordenades dimensionals (també anomenats components). Si ja coneixeu la longitud (magnitud) d'un vector, podeu ometre alguns dels passos següents.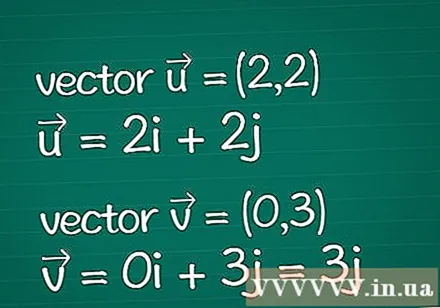
   • Exemple: vector bidimensional = (2,2) i vector bidimensional = (0,3). També es poden escriure com a = 2jo + 2j i = 0jo + 3j = 3j.
   • Tot i que a l'exemple d'aquest article s'utilitzen vectors bidimensionals, les instruccions següents es poden aplicar a vectors amb qualsevol nombre de dimensions.

2. 

   
   
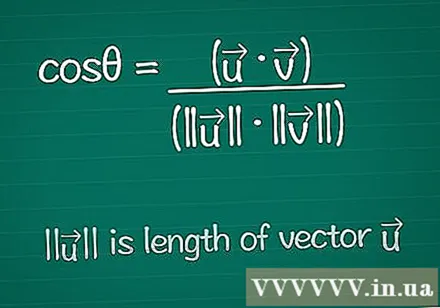
   Anota la fórmula del cosinus. Per trobar l’angle θ entre dos vectors, comencem per la fórmula per trobar el cosinus d’aquest angle. Podeu obtenir informació sobre aquesta fórmula a continuació o simplement escriure-la així:
   • cosθ = (•) / (|||| ||||)
   • |||| significa "longitud del vector".
   • • és el producte escalar dels dos vectors: això s'explicarà a continuació.

3. 

   
   
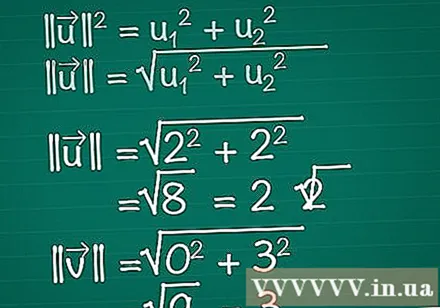
   Calculeu la longitud de cada vector. Imagineu-vos que un triangle rectangle està format pels components x, y del vector i el mateix vector. El vector forma la hipotenusa del triangle, de manera que per trobar la seva longitud fem servir el teorema de Pitagòrica. De fet, aquesta fórmula es pot ampliar fàcilment a un vector de qualsevol nombre de dimensions.
   • || u || = u₁ + u₂. Si un vector té més de dos elements, només heu de continuar afegint + u₃ + u₄ +...
   • Per tant, per a un vector bidimensional, || u || = √ (u₁ + u₂).
   • En aquest exemple, |||| = √ (2 + 2) = √ (8) = 2√2. |||| = √(0 + 3) = √(9) = 3.

4. 

   
   
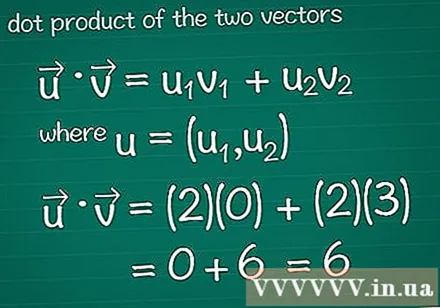
   Calculeu el producte escalar de dos vectors. Potser heu après el mètode de multiplicació vectorial, també conegut com escalar això. Per calcular el producte escalar en relació amb la seva composició, multipliqueu els ingredients en cada direcció i sumeu tot el resultat.
   • Per al programa de gràfics, consulteu Consells abans de continuar llegint.
   • En matemàtiques • = u₁v₁ + u₂v₂, on, u = (u₁, u₂). Si el vector té més de dos elements, simplement afegiu + u₃v₃ + u₄v₄...
   • En aquest exemple, • = u₁v₁ + u₂v₂ = (2)(0) + (2)(3) = 0 + 6 = 6. Aquest és el producte escalar del vector i del vector.

5. 

   Posa els resultats a la fórmula. Recordeu que cosθ = (•) / (|||| || ||). Ara coneixem tant el producte escalar com la longitud de cada vector. Introduïu-los a la fórmula per calcular el cosinus de l'angle.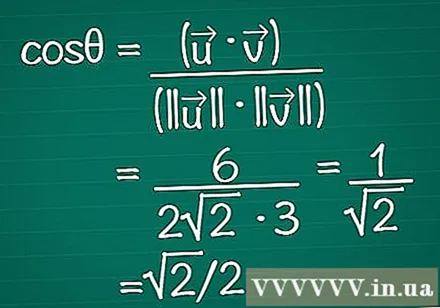
   • En el nostre exemple, cosθ = 6 / (2√2 * 3) = 1 / √2 = √2 / 2.

6. 

   Trobeu l’angle en funció del seu cosinus. Podeu utilitzar la funció arccos o cos en una calculadora per trobar θ a partir d’un valor de cos conegut. Amb alguns resultats, podeu trobar l’angle en funció del cercle de la unitat.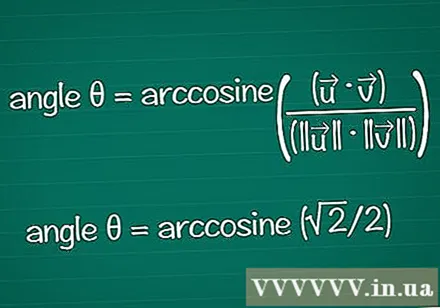
   • A l'exemple, cosθ = √2 / 2. Introduïu "arccos (√2 ​​/ 2)" a la calculadora per trobar l'angle. O bé, podeu trobar l’angle θ al cercle de la unitat, a la posició cosθ = √2 / 2. És cert per a θ = /₄ o 45º.
   • Combinant-ho tot, la fórmula final és: angle θ = arccosina ((•) / (|||| || ||))
   publicitat

Part 2 de 2: Determinació de la fórmula de l’angle

1. 

   Comprendre el propòsit de la fórmula. Aquesta fórmula no es va derivar de les regles existents. En el seu lloc, es forma com la definició del producte escalar i l’angle entre els dos vectors. Tot i això, no va ser una decisió arbitrària. Tornant a la geometria bàsica, podem entendre per què aquesta fórmula proporciona definicions intuïtives i útils.
   • Els exemples següents utilitzen vectors bidimensionals perquè són més fàcils d’entendre i més senzills. Els vectors tridimensionals o més tenen propietats definides per fórmules generals gairebé similars.

2. 

   Reviseu el teorema de Cosine. Considereu un triangle ordinari amb angle θ entre els costats a i b, costat oposat c. El teorema del cosinus afirma que c = a + b -2abcos(θ). Aquest resultat s’obté senzillament de la geometria bàsica.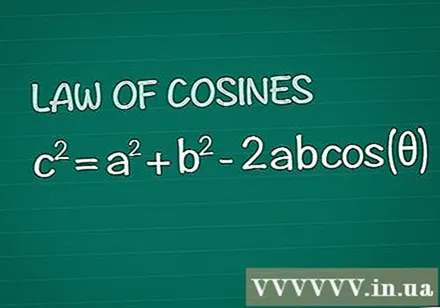

3. 

   Connecta dos vectors, formant un triangle. Dibuixa un parell de vectors bidimensionals sobre paper, vectors i vectors, essent θ l’angle entre ells. Dibuixa un tercer vector entre aquests dos per crear un triangle. En altres paraules, dibuixeu un vector tal que + =. Vector = -.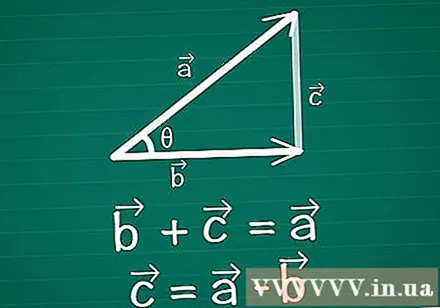

4. 

   Escriviu el teorema del cosinus d’aquest triangle. Substituïu la longitud del costat del nostre "triangle vectorial" pel teorema del cosinus:
   • || (a - b) || = || a || + || b || - 2 || a || || b ||cos(θ)

5. 

   Torna a escriure amb producte escalar. Recordeu, un producte escalar és la imatge d’un vector per l’altre. El producte escalar d’un vector amb ell mateix no requereix cap projecció, perquè aquí no hi ha diferències de direcció. Això significa • = || a ||. Amb això, reescrivim l’equació:
   • (-) • (-) = • + • - 2 || a || || b ||cos(θ)

6. 

   Heu tornat a escriure la mateixa fórmula. Amplieu la part esquerra de la fórmula i, a continuació, simplifiqueu-la per obtenir la fórmula que s’utilitza per trobar angles.
   • • - • - • + • = • + • - 2 || a || || b ||cos(θ)
   • - • - • = -2 || a || || b ||cos(θ)
   • -2 (•) = -2 || a || || b ||cos(θ)
   • • = || a || || b ||cos(θ)
   publicitat

Consells

• Per canviar valors i resoldre el problema ràpidament, utilitzeu aquesta fórmula per a qualsevol parell de vectors bidimensionals: cosθ = (u₁ • v₁ + u₂ • v₂) / (√ (u₁ • u₂) • √ (v₁ • v₂)).
• Si esteu treballant amb programari de gràfics per ordinador, és probable que només us hagueu de preocupar per la dimensió dels vectors sense preocupar-vos de la seva longitud. Seguiu els passos següents per escurçar una equació i accelerar el programa:
  • Normalitzeu cada vector de manera que siguin iguals a 1. Per fer-ho, dividiu cadascun dels components del vector per la seva longitud.
  • Obteniu el producte normalitzat de l'escalar en lloc del vector original.
  • Com que la longitud és 1, podem excloure els elements de longitud de l'equació. Finalment, l’equació d’angle obtinguda és arccos (•).
• Basant-nos en la fórmula del cosinus, podem determinar ràpidament si l’angle és agut o obtús. Comenceu per cosθ = (•) / (|||| ||||):
  • Els costats esquerre i dret de l’equació han de tenir el mateix signe (positiu o negatiu).
  • Com que la longitud sempre és positiva, cosθ ha de tenir el mateix signe que el producte escalar.
  • Per tant, si el producte és positiu, cosθ també és positiu. Estem al primer quadrant del cercle unitari, amb θ <π / 2 o 90º. L’angle a trobar és l’angle nítid.
  • Si el producte escalar és negatiu, cosθ és negatiu. Estem al segon quadrant del cercle unitari, amb π / 2 <θ ≤ π o 90º <θ ≤ 180º. Aquest és el racó de la presó.