Content

• Per trepitjar
• Part 1 de 3: Els fonaments de l'anàlisi
• Part 2 de 3: Entendre les derivades
• Part 3 de 3: Entendre les integrals
• Consells

L’anàlisi (també anomenat càlcul) és una branca de les matemàtiques centrada en límits, funcions, derivades, integrals i sèries infinites. Aquesta assignatura cobreix una gran quantitat de matemàtiques i es basa en moltes de les fórmules i equacions utilitzades en física i mecànica. Probablement haureu tingut diversos anys de matemàtiques a l’escola secundària per entendre correctament l’anàlisi, però aquest article us ajudarà a aprendre a reconèixer els conceptes clau i a comprendre millor la teoria.

Per trepitjar

Part 1 de 3: Els fonaments de l'anàlisi

1. L’anàlisi és l’estudi de com canvien les coses. L’anàlisi és una branca de les matemàtiques que examina nombres i gràfics, normalment extrets de dades del món real, i explica com canvien. Tot i que al principi això pot no semblar molt útil, l’anàlisi és una de les branques més utilitzades de les matemàtiques. Imagineu-vos tenir les eines per explicar-vos la rapidesa amb què creix el vostre negoci en cada moment, o com traçar el rumb d’una nau espacial i la rapidesa amb què s’està consumint el combustible. L’anàlisi és una eina important en enginyeria, economia, estadística, química i física, i ha contribuït a molts invents i descobriments.
2. Les funcions són relacions entre dos nombres i s’utilitzen per mapear relacions. Són regles per a la relació entre nombres i els matemàtics les utilitzen per fer gràfics. En una funció, cada entrada té exactament un resultat. Per exemple: in ${ displaystyle y = 2x + 4,}$Penseu en el concepte d’infinit. L’infinit és la repetició constant d’un procés. No és un lloc específic (no es pot anar a l'infinit), sinó el comportament d'un nombre o d'una equació, si es fa per sempre. Això és important per estudiar el canvi: és possible que vulgueu saber la velocitat amb què es mou el vostre cotxe en cada moment, però és la velocitat del vostre cotxe durant el segon actual? Mil·lisegons? Nanosegon? Podeu trobar trossos de temps infinitament més petits per ser encara més precisos, i és llavors quan entra l’anàlisi.
3. Comprendre el concepte de límits. Un límit indica què passa quan alguna cosa s’acosta a l’infinit. Agafeu el número 1 i dividiu-lo per 2. Segueu dividint per 2 una vegada i una altra. 1 es converteix en 1/2 i després en 1/4, 1/8, 1/16, 1/32, etc. Cada vegada que el nombre es fa més petit, "més a prop" de zero. Però on s’atura? Quantes vegades heu de dividir 1 per 2 per obtenir zero? En lloc de respondre a aquesta pregunta, en feu una anàlisi límit En aquest cas, el límit és.
   • Els límits són els més fàcils de visualitzar en un gràfic; per exemple, hi ha punts que un gràfic gairebé toca, però mai del tot?
   • Els límits poden ser nombre, infinits o fins i tot inexistents. Per exemple, amb la seqüència d'addició 1 + 2 + 2 + 2 + 2 + ... i això continua indefinidament, el nombre final es fa infinitament gran. El límit esdevé llavors infinit.
4. Reviseu els conceptes matemàtics essencials d’àlgebra, trigonometria i els fonaments de les matemàtiques. L’anàlisi es basa en bona part de les matemàtiques que heu après anteriorment. Estar ben informat sobre tots els temes facilita l’aprenentatge i la comprensió de l’anàlisi. Alguns temes a tractar són:
   • Àlgebra. Cal entendre els diferents processos i ser capaç de resoldre equacions i sistemes d’equacions amb múltiples variables. Comprendre els conceptes bàsics de les col·leccions. Practicar la creació de gràfics.
   • Geometria. La geometria és l’estudi de les formes. Hauríeu de tenir coneixements bàsics sobre triangles, rectangles i cercles i sobre com calcular coses com perímetre i àrea. Comprendre angles, línies i coordenades
   • Trigonometria. La trigonometria és la branca de les matemàtiques que tracta de les propietats dels cercles i dels triangles rectangles. Saber utilitzar identitats trigonomètriques, gràfics, funcions i funcions trigonomètriques inverses.
5. Compreu una calculadora gràfica. L’anàlisi no és fàcil d’entendre sense veure el que esteu fent. Les calculadores gràfiques fan que les funcions siguin visuals perquè pugueu entendre millor amb quines equacions es tracta. Sovint els límits també es mostren a la pantalla i les derivades i les funcions es calculen automàticament.
   • Actualment, molts telèfons intel·ligents i tauletes ofereixen aplicacions de gràfics econòmiques però efectives si no voleu o no podeu comprar una calculadora de gràfics.

Part 2 de 3: Entendre les derivades

1. L'anàlisi s'utilitza per estudiar el "canvi en un moment concret". Saber per què alguna cosa canvia en un moment exacte és el nucli de l’anàlisi. Per exemple, l'anàlisi no només proporciona la velocitat d'un cotxe, sinó també quant canvia aquesta velocitat en un moment donat. Aquest és un dels usos d'anàlisi més senzills, però molt important. Imagineu quina importància té aquesta informació per determinar la velocitat que es necessita per aconseguir que una nau espacial arribi a la Lluna.
   • La determinació del canvi en un moment determinat té diferenciar. La diferenciació és la primera de les dues grans branques d’anàlisi.
2. Utilitzeu derivats per entendre com canvien les coses en un moment determinat. Un "derivat" és una bona paraula que sovint posa els estudiants nerviosos. Tanmateix, el concepte en si no és tan difícil d’entendre, només significa "la rapidesa amb què canvia alguna cosa". Els derivats que més us trobareu a la vida quotidiana tenen a veure amb la velocitat. Tanmateix, normalment no en dieu "el derivat de la velocitat", sinó simplement "acceleració".
   • L’acceleració és una derivada: us indica la velocitat amb què una cosa s’accelera o disminueix o com canvia la seva velocitat.
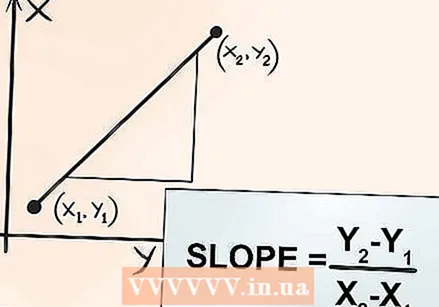3. Sabeu que la taxa de canvi és igual al pendent entre dos punts. Aquest és un dels descobriments d’anàlisi més importants. La taxa de variació entre dos punts és igual al pendent de la línia entre aquests dos punts. Només cal pensar en una línia simple, com la de l’equació 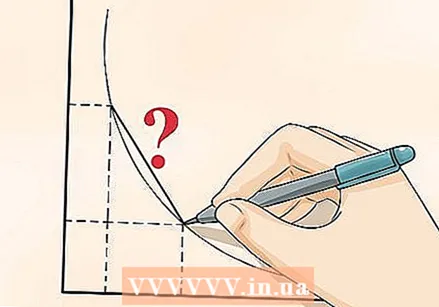${ displaystyle y = 3x.}$Sabeu que podeu determinar el pendent de les línies corbes. Determinar el pendent d’una línia recta és relativament fàcil: quant canvia 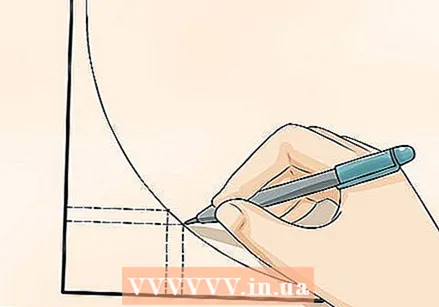${ displaystyle y}$Si voleu calcular el canvi amb més precisió, assegureu-vos que els punts estan més a prop els uns dels altres. Com més a prop escolliu els dos punts, més exacta serà la vostra resposta. Suposem que voleu saber quant accelera el vostre cotxe quan premeu l’accelerador. No voleu mesurar el canvi de velocitat entre la vostra casa i el supermercat, però sí el canvi de velocitat des del moment que colpeja l’accelerador. Com més s’acosti la lectura a aquesta fracció de segon, més precís serà el càlcul del canvi.
   • Per exemple, els científics estan investigant la rapidesa amb què algunes espècies s’extingeixen per salvar-les. Tot i això, a l’hivern moren més animals que a l’estiu, per la qual cosa no és útil estudiar la taxa de canvis al llarg de l’any; és millor determinar la taxa de canvi en un període inferior, com ara de l’1 de juliol a l’1 d’agost.
4. Utilitzeu línies infinitament curtes per determinar la "velocitat de canvi instantània" o trobeu la derivada. Aquí és on l’anàlisi sovint resulta una mica confús, però en realitat és el resultat de dos fets senzills. En primer lloc, ja sabeu que el pendent d’una línia és igual a la velocitat amb què canvia aquesta línia. En segon lloc, sabeu que com més a prop els punts de la línia estiguin entre ells, més precisa serà la lectura. Però, com es pot trobar la taxa de canvi en un punt determinat si el pendent és la relació entre dos punts? La resposta: Escolliu dos punts infinitament propers entre si.
   • Penseu en l'exemple en què continueu dividint 1 per 2, obtenint així 1/2, 1/4, 1/8, etc. Al final, doncs, s’acosta a zero i la resposta és “gairebé nul·la”. Els punts estan tan a prop l'un de l'altre que són "gairebé iguals". Aquesta és la naturalesa dels derivats.
5. Apreneu a determinar diverses derivades. Hi ha un munt de tècniques diferents per trobar una derivada en funció de l’equació, però la majoria tenen sentit si heu memoritzat els conceptes bàsics de les derivades anteriors. Totes les derivades són una manera de trobar el pendent d'una línia "infinitesimal". Ara que ja sabeu més sobre la teoria de les derivades, gran part del treball consisteix a trobar les respostes.
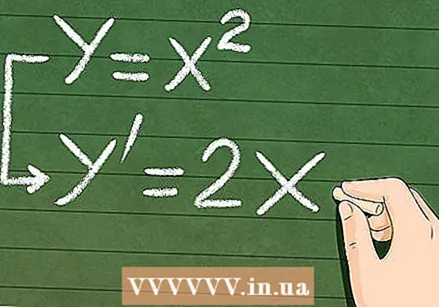6. Cerqueu les equacions derivades per predir la taxa de canvi en qualsevol moment. És útil fer servir derivats per determinar la velocitat de canvi en un moment donat, però la bellesa de l’anàlisi és que podeu crear un model nou per a qualsevol funció. La derivada de ${ displaystyle y = x ^ {2},}$Si us resulta difícil d’entendre, intenteu recordar exemples de derivats de la vida real. L’exemple més senzill es basa en la velocitat, que engloba moltes derivades diferents que ens trobem cada dia. No oblidis: una derivada és una mesura de la rapidesa amb què canvia alguna cosa. Penseu en un experiment senzill. Feu rodar un marbre sobre una taula i mesureu fins a quin punt es mou i la velocitat de cada vegada. Imagineu ara que el marbre rodant segueix una línia en un gràfic: utilitzeu derivades per mesurar els canvis instantanis en qualsevol moment en aquesta línia.
   • A quina velocitat es mou el marbre? A quina velocitat canvia la posició (o derivada) del marbre en moviment? A aquesta derivada l’anomenem “velocitat”.
   • Feu rodar el marbre per un pendent i observeu com canvia la velocitat. Quina és la velocitat de canvi, o derivada, de la velocitat del marbre? Aquesta derivada és el que anomenem "acceleració".
   • Feu rodar el marbre per una pista ondulada, com ara una muntanya russa. Fins a quin punt el marbre guanya velocitat quan roda cap avall i fins a quin punt el marbre disminueix la pujada? Quina velocitat fa exactament el marbre quan es troba a mitja pujada del primer turó? Aquesta és la velocitat de canvi instantània, o la derivada, d’aquest marbre en aquell punt concret.

Part 3 de 3: Entendre les integrals

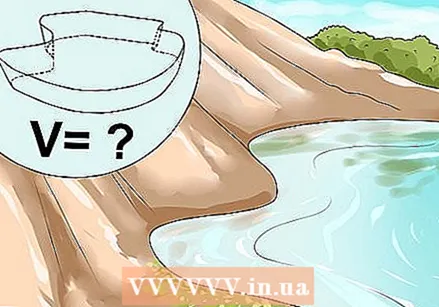1. Sabeu que podeu utilitzar l'anàlisi per trobar àrees i volums complexos. Amb l’anàlisi podeu mesurar formes complexes que, d’altra banda, són difícils de mesurar. Penseu, per exemple, en el problema que voleu saber quanta aigua conté un llac llarg de forma irregular: és impossible mesurar cada litre d’aigua per separat o utilitzar un regle per mesurar la forma del llac. Amb l’anàlisi podeu estudiar com canvien les vores del llac i, a continuació, utilitzar aquesta informació per esbrinar quanta aigua conté.
   • Realització de models geomètrics i estudi de volums integrar. El càlcul integrat és la segona branca d’anàlisi important.
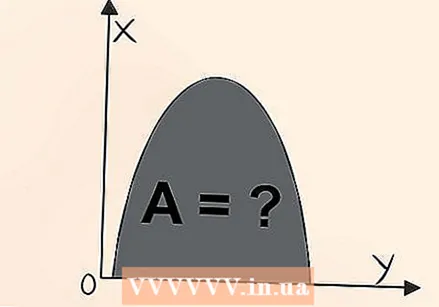2. Sabeu que la integració és l'àrea que hi ha a sota d'un gràfic. La integració s’utilitza per mesurar l’espai situat a sota d’una línia, cosa que permet determinar l’àrea de formes estranyes o irregulars. Pren l’equació 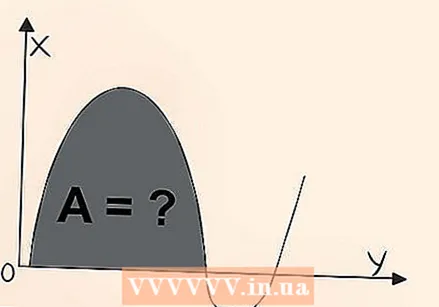${ displaystyle y = 4-x ^ {2},}$Sabeu que heu de seleccionar una àrea per integrar-la. No es pot integrar simplement una funció sencera. Per exemple, 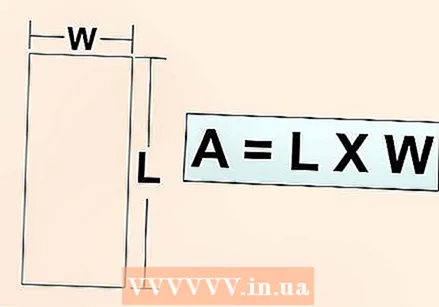${ displaystyle y = x}$Penseu en com calcular l'àrea d'un rectangle. Suposem que teniu una línia plana sobre un gràfic, com ara ${ displaystyle y = 4.}$Sabeu que en el càlcul integral s’uneixen molts rectangles petits per trobar l’àrea d’una àrea. Quan amplieu una corba enormement, sembla que és una línia recta. Ho veus cada dia: no pots percebre la curvatura de la terra perquè estàs molt a prop de la superfície terrestre. La integració crea un nombre infinit de petits rectangles sota una corba que són tan petits que bàsicament són plans, cosa que us permet comptar-los. Tots aquests rectangles sumats formen l'àrea de l'àrea sota una corba.
   • Suposem que sumeu molts segments petits a sota del gràfic, i això és l’amplada de cada segment gairebé és zero.
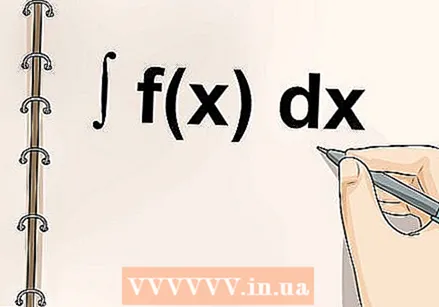3. Saber llegir i escriure integrals correctament. Les integrals consten de 4 parts. Una integral típica té aquest aspecte:
   
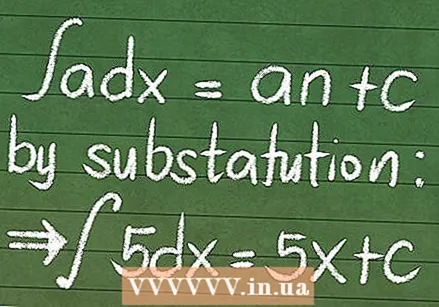   ${ displaystyle int f (x) mathrm {d} x}$ Obteniu més informació sobre com trobar integrals. La integració es presenta de moltes formes, i heu d’aprendre moltes fórmules diferents per integrar cada funció. Tot i això, tots segueixen els principis esmentats anteriorment: la integració és la suma d’un nombre infinit de coses.
   • Integrar per substitució.
   • Calculeu integrals indefinides.
   • Integrar-se compartint.
4. Saber que la integració és el revers de la diferenciació i viceversa. Aquesta és una regla general d’anàlisi que és tan important que se li ha donat el seu propi nom: el Teorema Principal del Càlcul Integral.Com que la integració i la diferenciació estan tan relacionades, es pot utilitzar una combinació de tots dos per determinar la velocitat de canvi, acceleració, velocitat, ubicació, moviment, etc., independentment de la informació que tingueu.
   • Per exemple, recordeu que la derivada de la velocitat és l’acceleració, de manera que podeu utilitzar la velocitat per trobar l’acceleració. Però si només coneixeu l’acceleració d’alguna cosa (com ara objectes que cauen a causa de la gravetat), podeu integrar-vos per recuperar la velocitat.
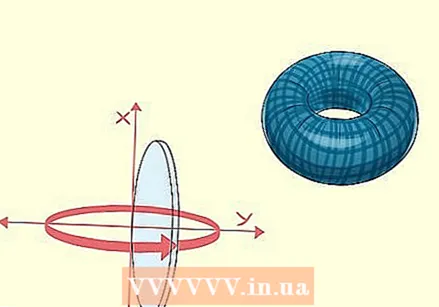5. Sabeu que amb la integració també podeu controlar el volum d’objectes en 3D. Girar una forma plana és una manera de crear sòlids en 3D. Imagineu com una moneda gira sobre la taula: observeu com sembla que la moneda pren la forma d’una esfera a mesura que gira. Aquest concepte permet determinar el volum segons un procés conegut com a "volum per rotació".
   • Això us permet determinar el volum de qualsevol sòlid, sempre que tingueu una funció que el representi. Per exemple, podeu crear una funció que faci un seguiment del fons d’un llac i després utilitzar-la per determinar el volum del llac o la quantitat d’aigua que conté.

Consells

• La pràctica és perfecta, així que feu els exercicis pràctics del vostre llibre de text (fins i tot aquells que el vostre professor no ha donat) i comproveu les respostes per ajudar-vos a entendre millor els conceptes.
• Si no trobeu una solució, pregunteu-ho al vostre professor.