Content

• Per trepitjar
• Mètode 1 de 3: una primera tasca senzilla
• Mètode 2 de 3: càlcul del valor esperat per a un resultat específic
• Mètode 3 de 3: entendre el concepte
• Consells
• Necessitats

El valor de l’expectativa és un terme estadístic i un concepte que s’utilitza per decidir la utilitat o la nocivitat d’una acció. Per calcular el valor esperat, és necessari obtenir una bona comprensió de cada resultat en una situació particular i la probabilitat associada, o la probabilitat que es produeixi un resultat concret. Els passos següents ofereixen alguns exemples d'exercicis per ajudar-vos a entendre el concepte del valor expectatiu.

Per trepitjar

Mètode 1 de 3: una primera tasca senzilla

1. Llegiu l’enunciat. Abans de començar a pensar en tots els possibles resultats i probabilitats, és important que entengueu el problema. Per exemple, un joc de daus que costa 10 € per partida. Un dau hexagonal es llença una vegada i els seus guanys depenen del nombre que es llenci. Si es tira un 6, guanyeu 30 €; un 5 guanya 20 €; qualsevol altre número no produeix res.
2. Enumereu tots els resultats possibles. Ajuda a enumerar tots els resultats possibles en una situació determinada. A l'exemple anterior, hi ha 6 possibles resultats. Aquests són: (1) tirar un 1 i perdre $ 10, (2) tirar un 2 i perdre $ 10, (3) tirar un 3 i perdre $ 10, (4) tirar un 4 i perdre $ 10 , (5) tira un 5 i guanya 10 $, (6) tira un 6 i guanya 20 $.
   • Tingueu en compte que cada resultat és de 10 € menys del descrit anteriorment, ja que primer haureu de pagar 10 € per partit, independentment del resultat.
3. Determineu la probabilitat de cada resultat. En aquest cas, la probabilitat de 6 resultats és la mateixa. La probabilitat que es llanci un número aleatori és d’1 en 6. Per fer-ho més fàcil d’escriure, escriurem la fracció (1/6) com a decimal mitjançant una calculadora: 0,167. Escriviu aquesta probabilitat al costat de cada resultat, sobretot si voleu resoldre un problema amb probabilitats diferents per a cada resultat.
   • La vostra calculadora 1/6 pot fer alguna cosa com 0.166667. Arredonem això a 0,167 per facilitar el càlcul sense sacrificar la precisió.
   • Si voleu un resultat molt precís, no el converteix en un decimal, només cal introduir 1/6 a la fórmula i calcular-lo a la calculadora.
4. Anoteu el valor de cada resultat. Multipliqueu el dòlar d'un resultat per la probabilitat que es produeixi el resultat per calcular quants diners aportarà aquest resultat al valor esperat. Per exemple, el resultat de rodar un 1 és de - $ 10 i la probabilitat de rodar un 1 és de 0,167. Per tant, el valor de llançar un 1 és (-10) * (0,167).
   • Ara no cal calcular aquests resultats si teniu una calculadora que pot realitzar diverses operacions alhora. Si introduïu tota l’equació, obtindreu un resultat més precís.
5. Afegiu el valor de cada resultat per obtenir el valor esperat d'un esdeveniment. Per continuar amb l'exemple anterior, el valor esperat del joc de daus és: (-10 * 0.167) + (-10 * 0.167) + (-10 * 0.167) + (-10 * 0.167) + (10 * 0,167) + (20 * 0,167), o bé - 1,67 €. Per tant, podeu esperar a perdre 1,67 dòlars cada vegada en aquest joc (per partit).
6. Quines són les implicacions del càlcul del valor esperat. A l'exemple anterior, vam determinar que el benefici (pèrdua) esperat seria d'1,67 € per llançament. Aquest és un resultat impossible per a 1 partit; podeu perdre 10 €, guanyar 10 € o guanyar 20 €. Però, a la llarga, el valor esperat és una probabilitat mitjana i útil. Si continueu jugant a aquest joc, perdreu aproximadament 1,67 dòlars per partit, de mitjana. Una altra manera de pensar el valor esperat és assignant determinats costos (o beneficis) al joc; només hauríeu de jugar a aquest joc si ho pagueu la pena, gaudiu-ne prou per gastar-hi 1,67 dòlars cada vegada.
   • Com més sovint es repeteixi una situació, amb més precisió el valor esperat és una representació del resultat mitjà real. Per exemple, potser jugueu el joc 5 vegades seguides i perdeu cada vegada, cosa que provoca una pèrdua mitjana de 10 dòlars. Tanmateix, si jugueu el joc 1000 vegades més, el resultat mitjà s’acostarà cada cop més al valor esperat de: 1,67 € per partit. Aquest principi s’anomena “la llei dels grans nombres”.

Mètode 2 de 3: càlcul del valor esperat per a un resultat específic

1. Utilitzeu aquest mètode per calcular el nombre mitjà de monedes que heu de tirar abans que es produeixi un patró concret. Per exemple, podeu utilitzar el mètode per esbrinar el nombre esperat de monedes que es volen tirar fins que tingueu caps dos cops seguits. Aquest problema és una mica més complicat que un problema estàndard sobre valors d’expectativa, per tant, llegiu primer la part anterior d’aquest article si no esteu familiaritzat amb el concepte de valor d’espera.
2. Suposem que busquem un valor x. Esteu intentant determinar quantes monedes heu de tirar de mitjana per aconseguir dos caps seguits. Ara fem una comparació per trobar la resposta. Anomenem x la resposta que busquem. Fem la comparació necessària pas a pas. Actualment disposem del següent:
   • x = ___
3. Penseu en què passa si la primera tirada produeix una moneda. Aquest serà el cas en la meitat dels casos. Si aquest és el cas, heu "malgastat" un tomb, mentre que l'oportunitat de rodar un cap dues vegades seguides no ha canviat. Igual que amb el llançament de monedes, s’espera que hagueu de llançar un nombre mitjà de vegades abans d’obtenir un cap dues vegades seguides. Dit d’una altra manera, s’esperava rodar un x nombre de vegades, més les que ja heu jugat. En forma d’equació:
   • x = (0,5) (x + 1) + ___
   • Omplirem l’espai buit mentre continuem pensant en altres situacions.
   • Podeu utilitzar fraccions en lloc de decimals si és més fàcil o necessari.
4. Penseu en què passa quan llenceu el cap. Hi ha 0,5 (o 1/2) possibilitats que llenceu una tassa la primera vegada. Sembla que això s’acosta a l’objectiu de llançar el cap dues vegades seguides, però quant? La forma més senzilla d’esbrinar-ho és pensar en les vostres opcions al segon tiratge:
   • Si el segon llançament és una moneda, tornem al principi.
   • Si la segona vegada també és una copa, ja hem acabat!
5. Apreneu a calcular la probabilitat que es produeixin dos esdeveniments. Ara sabem que teniu un 50% de probabilitats de llançar una tassa, però quina és la possibilitat que llenceu una tassa dues vegades seguides? Per calcular aquesta probabilitat, multipliqueu la probabilitat d’ambdues. En aquest cas és de 0,5 x 0,5 = 0,25. Per descomptat, aquesta és també la possibilitat que feu rodar caps i després cues, perquè tots dos tenen la possibilitat que es produeixi 0,5: 0,5 x 0,5 = 0,25.
6. Afegiu el resultat de "caps, després cues" a l'equació. Ara que hem calculat la probabilitat que es produeixi aquest esdeveniment, podem passar a expandir l’equació. Hi ha 0,25 (o 1/4) de probabilitats que malgastem tirant dues vegades sense avançar. Però ara encara necessitem un nombre x de llançaments més de mitjana per obtenir el resultat que volem obtenir, més els 2 que ja hem llançat. En forma d’equació, es converteix en (0,25) (x + 2), que ara podem afegir a l’equació:
   • x = (0,5) (x + 1) + (0,25) (x + 2) + ___
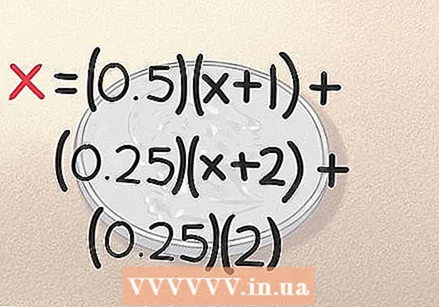7. Afegiu el resultat de "encapçalament, encapçalament" a l'equació. Si feu rodar el cap, dirigiu-vos amb els dos primers llançaments de les monedes, ja heu acabat. Heu obtingut el resultat en exactament 2 llançaments. Com hem assenyalat anteriorment, hi ha una probabilitat de 0,25 que això passi, de manera que l’equació per a això és (0,25) (2). La nostra comparació ja és completa:
   • x = (0,5) (x + 1) + (0,25) (x + 2) + (0,25) (2)
   • Si no esteu segur d’haver pensat en totes les situacions possibles, hi ha una manera fàcil de comprovar que l’equació està completa. El primer número de cada part de l’equació representa la probabilitat que es produeixi un esdeveniment. Això sempre sumarà 1. Aquí, 0,5 + 0,25 + 0,25 = 1, de manera que sabem que hem inclòs totes les situacions.
8. Simplifiqueu l’equació. Fem la equació una mica més fàcil multiplicant-la. Recordeu, si veieu alguna cosa entre parèntesis com aquest: (0,5) (x + 1), multiplicareu 0,5 per cada terme que es troba al segon conjunt de parèntesis. Això us proporciona el següent: 0,5x + (0,5) (1) o 0,5x + 0,5. Fem-ho per a cada terme de l'equació i, a continuació, combinem aquests termes perquè tot sembli una mica més senzill:
   • x = 0,5x + (0,5) (1) + 0,25x + (0,25) (2) + (0,25) (2)
   • x = 0,5x + 0,5 + 0,25x + 0,5 + 0,5
   • x = 0,75x + 1,5
9. Resol per x. Com en qualsevol equació, haureu d’aïllar la x en un costat de l’equació per calcular-la. Recordeu, x significa "el nombre mitjà de monedes que heu de llançar per obtenir caps dos cops seguits". Quan hem calculat x, també hem trobat la nostra resposta.
   • x = 0,75x + 1,5
   • x - 0,75x = 0,75x + 1,5 - 0,75x
   • 0,25x = 1,5
   • (0,25x) / (0,25) = (1,5) / (0,25)
   • x = 6
   • De mitjana, haureu de llançar una moneda 6 vegades abans de llançar el cap dues vegades.

Mètode 3 de 3: entendre el concepte

1. Quin és un valor esperat en realitat. El valor esperat no és necessàriament el resultat més evident o lògic. De vegades, un valor expectatiu pot ser fins i tot un valor impossible en una situació determinada. Per exemple, el valor previst pot ser de + 5 € per a un joc amb un premi no superior a 10 €. El que indica el valor expectatiu és el valor que té un esdeveniment concret. Si un joc té un valor esperat de + 5 €, podeu jugar-hi si creieu que val la pena el temps i els diners que podeu obtenir per partit. Si un altre joc té un valor esperat de - 20 $, només el jugarà si creieu que cada joc val 20 $.
2. Comprendre el concepte d’esdeveniments independents. A la vida quotidiana, molts de nosaltres creiem que tenim un dia de sort quan passen algunes coses bones i esperem que la resta del dia vagi per aquest camí.De la mateixa manera, podem pensar que ja hem tingut prou accident i que ara cal fer alguna cosa divertida. Matemàticament, les coses no van així. Si llanceu una moneda normal, hi ha exactament la mateixa possibilitat que llenceu un cap o una moneda. No importa quantes vegades ja hagis llançat; la propera vegada que llanceu, encara funcionarà de la mateixa manera. El llançament de monedes és "independent" de la resta de llançaments, no en queda afectat.
   • La creença que es pot tenir sort o mala sort en llançar monedes (o qualsevol altre joc d'atzar), o bé El fet que ara hagi acabat tota la vostra mala sort i que tingueu la sort al vostre costat també s’anomena engany dels jugadors (o fal·làcia del jugador). Això té a veure amb la tendència de la gent a prendre decisions arriscades o estúpides quan senten que la sort està del seu costat, o si se senten "ratxes de sort" o si senten que la seva "sort està a punt de convertir-se".
3. Comprendre la llei del gran nombre. Podríeu pensar que el valor expectatiu no és realment útil, perquè poques vegades us indica quin és el resultat real d’una situació. Si heu calculat que el valor esperat d'un joc de ruleta és de - 1 € i jugueu el joc 3 vegades, normalment acabareu amb - 10 €, o + 60 €, o algun altre resultat. La "Llei dels grans nombres" ajuda a explicar per què el valor expectatiu és més útil del que es podria pensar: com més jugueu, més a prop del valor expectatiu serà el resultat mitjà. Quan mireu el gran nombre d’esdeveniments, hi ha moltes possibilitats que el resultat final s’acosti al valor esperat.

Consells

• En aquelles situacions en què són possibles diversos resultats, podeu crear un full de càlcul a l'ordinador per calcular el valor esperat utilitzant els resultats i les seves probabilitats.
• Els càlculs en euros anteriors també funcionen en altres monedes.

Necessitats

• Llapis
• Paper
• Calculadora