Content

• Passos
• Mètode 1 de 3: càlcul de la pendent de l'equació d'una línia
• Mètode 2 de 3: Calculeu la pendent utilitzant dos punts
• Mètode 3 de 3: Ús del càlcul diferencial per calcular la pendent

El pendent caracteritza l’angle d’inclinació de la línia recta cap a l’eix d’abscisses (el pendent és numèricament igual a la tangent d’aquest angle). El pendent és present en l’equació d’una recta i s’utilitza en l’anàlisi matemàtica de corbes, on sempre és igual a la derivada d’una funció. Per facilitar la comprensió del pendent, imagineu-vos que afecta la velocitat de canvi de la funció, és a dir, com més gran sigui el valor de la pendent, més gran serà el valor de la funció (pel mateix valor de la variable independent).

Passos

Mètode 1 de 3: càlcul de la pendent de l'equació d'una línia

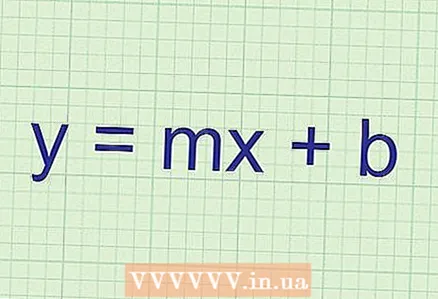1. 1 Utilitzeu el pendent per trobar l’angle de la línia amb l’abscissa i la direcció d’aquesta línia. Calcular el pendent és bastant fàcil si se us dóna l'equació d'una línia recta. Recordeu que en qualsevol equació de línia recta:
   • Sense exponents
   • Només hi ha dues variables, cap de les quals és fracció (per exemple, tal ${ displaystyle { frac {1} {x}}}$)
   • L’equació de la línia recta té la forma ${ displaystyle y = kx + b}$, on k i b són coeficients numèrics (per exemple, 3, 10, -12, ${ displaystyle { frac {4} {3}}}$).
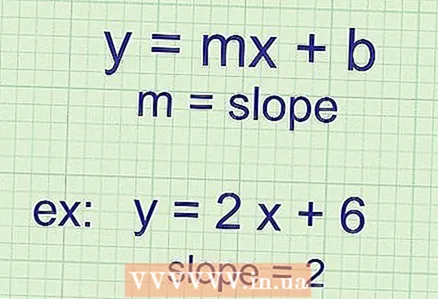2. 2 Per trobar el pendent, heu de trobar el valor de k (coeficient en "x"). Si l'equació que se us dóna té la forma ${ displaystyle y = kx + b}$, doncs, per trobar el pendent només heu de mirar el número que hi ha davant de la "x". Tingueu en compte que k (pendent) sempre està a la variable independent (en aquest cas, "x"). Si esteu confós, consulteu els exemples següents:
   • ${ displaystyle y = 2x + 6}$
     • Pendent = 2
   • ${ displaystyle y = 2-x}$
     • Pendent = -1
   • ${ displaystyle y = { frac {3} {8}} x-10}$
     • Pendent = ${ displaystyle { frac {3} {8}}}$
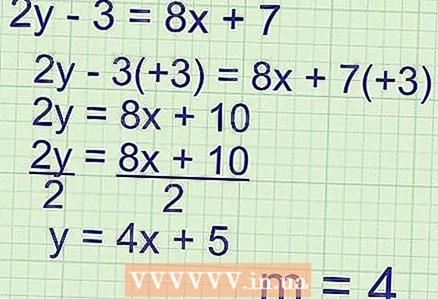3. 3 Si l'equació que se us dóna té una forma diferent de y=kx+b{ displaystyle y = kx + b}, aïlla la variable dependent. En la majoria dels casos, la variable dependent es denota com "y" i, per aïllar-la, podeu realitzar operacions de suma, resta, multiplicació i altres. Recordeu que qualsevol operació matemàtica s’ha de realitzar a banda i banda de l’equació (per no canviar el seu valor original). Heu d’aportar qualsevol formulari al formulari ${ displaystyle y = kx + b}$... Considerem un exemple:
   • Trobeu el pendent de l’equació ${ displaystyle 2y-3 = 8x + 7}$
   • Cal portar aquesta equació a la forma ${ displaystyle y = kx + b}$:
     • ${ displaystyle 2y-3 (+3) = 8x + 7 (+3)}$
     • ${ displaystyle 2y = 8x + 10}$
     • ${ displaystyle { frac {2y} {2}} = { frac {8x + 10} {2}}}$
     • ${ displaystyle y = 4x + 5}$
   • Trobar el pendent:
     • Pendent = k = 4

Mètode 2 de 3: Calculeu la pendent utilitzant dos punts

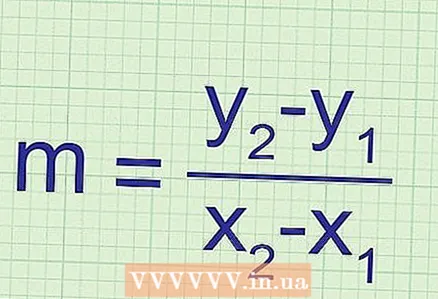1. 1 Utilitzeu el gràfic i dos punts per calcular el pendent. Si se us acaba de donar un gràfic d'una funció (sense equació), encara podreu trobar el pendent. Per fer-ho, necessiteu les coordenades de dos punts en aquest gràfic; les coordenades se substitueixen a la fórmula: ${ displaystyle { frac {y_ {2} -y_ {1}} {x_ {2} -x_ {1}}}}$... Per evitar errors en calcular el pendent, recordeu el següent:
   • Si el gràfic augmenta, el pendent serà positiu.
   • Si el gràfic és decreixent, el pendent és negatiu.
   • Com més gran sigui el valor de la pendent, més forta serà la gràfica (i viceversa).
   • El pendent d’una recta paral·lela a l’eix d’abscisses és 0.
   • El pendent d’una recta paral·lela a l’ordenada no existeix (és infinit).
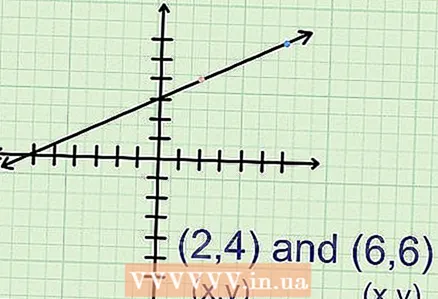2. 2 Trobeu les coordenades de dos punts. Al gràfic, marqueu dos punts qualsevol i trobeu les seves coordenades (x, y). Per exemple, els punts A (2.4) i B (6.6) són al gràfic.
   • En un parell de coordenades, el primer número correspon a "x" i el segon a "y".
   • Cada valor "x" correspon a un valor "y" determinat.
3. 3 Equivaleu x₁, y₁, x₂, y₂ als valors corresponents. En el nostre exemple amb els punts A (2,4) i B (6,6):
   • x₁: 2
   • y₁: 4
   • x₂: 6
   • y₂: 6
4. 4 Connecteu els valors trobats a la fórmula del pendent. Per trobar el pendent, s’utilitzen les coordenades de dos punts i s’utilitza la fórmula següent: ${ displaystyle { frac {y_ {2} -y_ {1}} {x_ {2} -x_ {1}}}}$... Connecteu les coordenades de dos punts.
   • Dos punts: A (2.4) i B (6.6).
   • Substituïu les coordenades dels punts per la fórmula:
     • ${ displaystyle { frac {6-4} {6-2}}}$
   • Simplifiqueu una resposta definitiva:
     • ${ displaystyle { frac {2} {4}} = { frac {1} {2}}}$ = Pendent
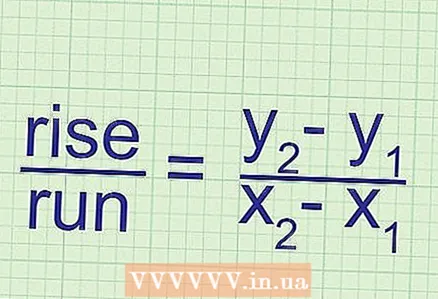5. 5 Explicació de l’essència de la fórmula. El pendent és igual a la proporció del canvi de la coordenada "y" (dos punts) al canvi de la coordenada "x" (dos punts). El canvi de coordenades és la diferència entre els valors de la coordenada corresponent del primer i segon punt.
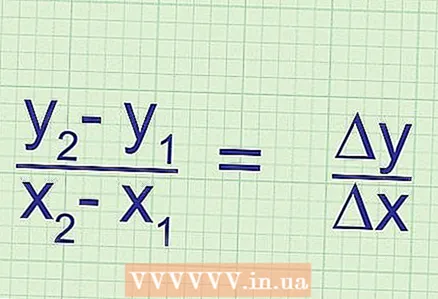6. 6 Un altre tipus de fórmula per calcular el pendent. La fórmula estàndard per calcular el pendent és: k = ${ displaystyle { frac {y_ {2} -y_ {1}} {x_ {2} -x_ {1}}}}$... Però pot tenir la forma següent: k = Δy / Δx, on Δ és la lletra grega "delta" que denota la diferència en matemàtiques. És a dir, Δx = x_2 - x_1 i Δy = y_2 - y_1.

Mètode 3 de 3: Ús del càlcul diferencial per calcular la pendent

1. 1 Apreneu a prendre derivades de funcions. La derivada caracteritza la velocitat de canvi d'una funció en un punt determinat situat al gràfic d'aquesta funció. En aquest cas, el gràfic pot ser una línia recta o corba. És a dir, la derivada caracteritza la velocitat de canvi de la funció en un moment concret del temps. Recordeu les regles generals per les quals es prenen les derivades i només després passeu al següent pas.
   • Llegiu l'article Com prendre un derivat.
   • En aquest article es descriu com prendre les derivades més simples, per exemple, la derivada de l’equació exponencial. Els càlculs presentats en els passos següents es basaran en els mètodes que s’hi descriuen.
2. 2 Apreneu a distingir entre problemes en què cal calcular el pendent en funció de la derivada d’una funció. En problemes no sempre es proposa trobar el pendent o la derivada d’una funció. Per exemple, se us pot demanar que trobeu la velocitat de canvi d'una funció en el punt A (x, y). També se us pot demanar que trobeu el pendent de la tangent al punt A (x, y). En ambdós casos, cal agafar la derivada de la funció.
   • Per exemple, trobeu el pendent d'una funció ${ displaystyle f (x) = 2x ^ {2} + 6x}$ al punt A (4.2).
   • El derivat sovint es denota com ${ displaystyle f '(x), y',}$ o bé ${ displaystyle { frac {dy} {dx}}}$
3. 3 Agafeu la derivada de la funció que se us ha donat. Aquí no cal representar un gràfic: només necessiteu l'equació de la funció. En el nostre exemple, prenem la derivada de la funció ${ displaystyle f (x) = 2x ^ {2} + 6x}$... Agafeu la derivada segons els mètodes descrits a l'article esmentat anteriorment:
   • Derivada: ${ displaystyle f ’(x) = 4x + 6}$
4. 4 Substituïu les coordenades del punt donat per la derivada derivada per calcular el pendent. La derivada de la funció és igual al pendent en un punt determinat. En altres paraules, f '(x) és el pendent de la funció en qualsevol punt (x, f (x)). En el nostre exemple:
   • Cerqueu el pendent de la funció ${ displaystyle f (x) = 2x ^ {2} + 6x}$ al punt A (4.2).
   • Derivada de la funció:
     • ${ displaystyle f ’(x) = 4x + 6}$
   • Substituïu el valor per la coordenada x d'aquest punt:
     • ${ displaystyle f ’(x) = 4 (4) +6}$
   • Cerqueu el pendent:
   • Pendent de funció ${ displaystyle f (x) = 2x ^ {2} + 6x}$ al punt A (4.2) és 22.
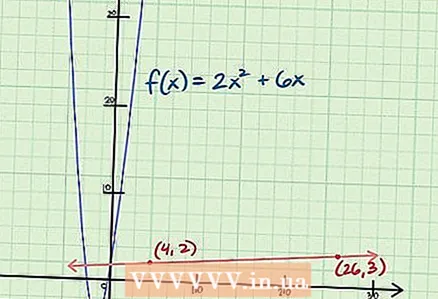5. 5 Si és possible, consulteu la resposta al gràfic. Recordeu que és possible que la pendent no es calculi en cada punt. El càlcul diferencial considera funcions complexes i gràfics complexos, on el pendent no es pot calcular en tots els punts, i en alguns casos els punts no es troben en absolut als gràfics. Si és possible, utilitzeu una calculadora gràfica per comprovar que el pendent s'està calculant correctament per a la funció que se us ha donat.En cas contrari, dibuixeu una tangent al gràfic en el punt donat i considereu si el valor de pendent que heu trobat coincideix amb el que veieu al gràfic.
   • La tangent tindrà el mateix pendent que el gràfic de funcions en un punt concret. Per dibuixar una tangent en un punt determinat, moveu-vos a la dreta / esquerra al llarg de l'eix X (en el nostre exemple, 22 valors a la dreta) i, a continuació, pugeu una unitat al llarg de l'eix Y. Marqueu el punt i, a continuació, connecteu-lo al punt que se us ha proporcionat. En el nostre exemple, connecteu els punts a les coordenades (4,2) i (26,3).