Content

• Passos
• Consells

La gràfica d’una equació quadràtica de la forma ax + bx + c o a (x - h) + k és una paràbola (corba en forma d’U). Per representar aquesta equació, heu de trobar el vèrtex de la paràbola, la seva direcció i els punts d’intersecció amb els eixos X i Y. Si se us dóna una equació quadràtica relativament senzilla, podeu substituir diferents valors de "x "en ell, trobeu els valors corresponents de" y "i creeu un gràfic ...

Passos

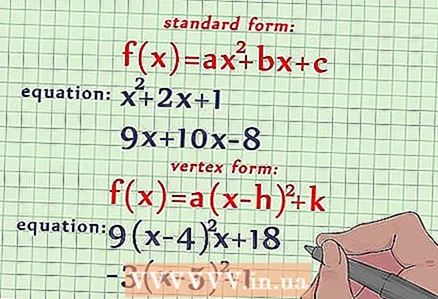1. 1 L'equació quadràtica es pot escriure en una forma estàndard i en una forma no estàndard. Podeu utilitzar qualsevol tipus d’equació per traçar una equació de segon grau (el mètode de traçat és lleugerament diferent). Com a regla general, en els problemes, les equacions de segon grau es donen de forma estàndard, però aquest article us explicarà els dos tipus d’escriptura d’una equació de segon grau.
   • Forma estàndard: f (x) = ax + bx + c, on a, b, c són nombres reals i a ≠ 0.
     • Per exemple, dues equacions de la forma estàndard: f (x) = x + 2x + 1 i f (x) = 9x + 10x -8.
   • Forma no estàndard: f (x) = a (x - h) + k, on a, h, k són nombres reals i a ≠ 0.
     • Per exemple, dues equacions d’una forma no estàndard: f (x) = 9 (x - 4) + 18 i -3 (x - 5) + 1.
   • Per traçar una equació quadràtica de qualsevol tipus, primer heu de trobar el vèrtex de la paràbola, que té coordenades (h, k). Les coordenades del vèrtex de la paràbola en les equacions de la forma estàndard es calculen mitjançant les fórmules: h = -b / 2a i k = f (h); les coordenades del vèrtex de la paràbola en equacions de forma no estàndard es poden obtenir directament a partir de les equacions.
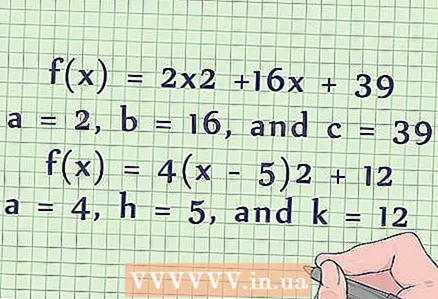2. 2 Per representar el gràfic, heu de trobar els valors numèrics dels coeficients a, b, c (o a, h, k). En la majoria de problemes, les equacions de segon grau es donen amb valors numèrics dels coeficients.
   • Per exemple, a l’equació estàndard f (x) = 2x + 16x + 39 a = 2, b = 16, c = 39.
   • Per exemple, en una equació no estàndard f (x) = 4 (x - 5) + 12, a = 4, h = 5, k = 12.
3. 3 Calculeu h en l'equació estàndard (en la no estàndard ja es dóna) utilitzant la fórmula: h = -b / 2a.
   • En el nostre exemple d’equació estàndard, f (x) = 2x + 16x + 39 h = -b / 2a = -16/2 (2) = -4.
   • En el nostre exemple d’equació no estàndard, f (x) = 4 (x - 5) + 12 h = 5.
4. 4 Calculeu k en l'equació estàndard (en la no estàndard ja està donada). Recordeu que k = f (h), és a dir, podeu trobar k substituint el valor trobat de h en lloc de "x" a l'equació original.
   • Heu trobat que h = -4 (per a l'equació estàndard). Per calcular k, substituïu aquest valor per "x":
     • k = 2 (-4) + 16 (-4) + 39.
     • k = 2 (16) - 64 + 39.
     • k = 32 - 64 + 39 = 7
   • En una equació no estàndard, k = 12.
5. 5 Dibuixa un vèrtex amb coordenades (h, k) al pla de coordenades. h es representa al llarg de l’eix X i k es representa al llarg de l’eix Y. La part superior d’una paràbola és el punt més baix (si la paràbola apunta cap amunt) o el punt més alt (si la paràbola apunta cap avall).
   • En el nostre exemple d’equació estàndard, el vèrtex té coordenades (-4, 7). Dibuixeu aquest punt al pla de coordenades.
   • En el nostre exemple d’equació personalitzada, el vèrtex té coordenades (5, 12). Dibuixeu aquest punt al pla de coordenades.
6. 6 Dibuixeu l'eix de simetria de la paràbola (opcional). L’eix de simetria passa per l’àpex de la paràbola paral·lel a l’eix Y (és a dir, estrictament vertical). L’eix de simetria divideix la paràbola per la meitat (és a dir, la paràbola és simètrica al mirall respecte d’aquest eix).
   • En el nostre exemple d’equació estàndard, l’eix de simetria és una línia recta paral·lela a l’eix Y i que passa pel punt (-4, 7). Tot i que aquesta línia no forma part de la paràbola en si, dóna una idea de la simetria de la paràbola.
7. 7 Determineu la direcció de la paràbola cap amunt o cap avall. Això és molt fàcil de fer.Si el coeficient "a" és positiu, la paràbola es dirigeix ​​cap amunt i, si el coeficient "a" és negatiu, la paràbola es dirigeix ​​cap avall.
   • En el nostre exemple de l’equació estàndard, f (x) = 2x + 16x + 39, la paràbola apunta cap amunt, ja que a = 2 (coeficient positiu).
   • En el nostre exemple d'una equació no estàndard f (x) = 4 (x - 5) + 12, la paràbola també es dirigeix ​​cap amunt, ja que a = 4 (coeficient positiu).
8. 8 Si cal, localitzeu i traqueu la intersecció x. Aquests punts us ajudaran molt a l’hora de dibuixar una paràbola. N’hi pot haver dos, un o cap (si la paràbola està dirigida cap amunt i el seu vèrtex es troba per sobre de l’eix X o si la paràbola es dirigeix ​​cap avall i el seu vèrtex es troba per sota de l’eix X). Per calcular les coordenades dels punts d'intersecció amb l'eix X, feu el següent:
   • Estableix l’equació a zero: f (x) = 0 i resol-la. Aquest mètode funciona amb equacions de segon grau senzilles (especialment les no estàndard), però pot ser extremadament difícil per a equacions complexes. En el nostre exemple:
     • f (x) = 4 (x - 12) - 4
     • 0 = 4 (x - 12) - 4
     • 4 = 4 (x - 12)
     • 1 = (x - 12)
     • √1 = (x - 12)
     • +/- 1 = x -12. Els punts d'intersecció de la paràbola amb l'eix X tenen coordenades (11,0) i (13,0).
   • Factoreu l’equació quadràtica de forma estàndard: ax + bx + c = (dx + e) ​​(fx + g), on dx × fx = ax, (dx × g + fx × e) = bx, e × g = c. A continuació, configureu cada binomi a 0 i cerqueu els valors de "x". Per exemple:
     • x + 2x + 1
     • = (x + 1) (x + 1)
     • En aquest cas, hi ha un únic punt d’intersecció de la paràbola amb l’eix x amb coordenades (-1,0), perquè a x + 1 = 0 x = -1.
   • Si no podeu factoritzar l'equació, resoleu-la mitjançant la fórmula quadràtica: x = (-b +/- √ (b - 4ac)) / 2a.
     • Per exemple: -5x + 1x + 10.
     • x = (-1 +/- √ (1 - 4 (-5) (10))) / 2 (-5)
     • x = (-1 +/- √ (1 + 200)) / - 10
     • x = (-1 +/- √ (201)) / - 10
     • x = (-1 +/- 14.18) / - 10
     • x = (13,18 / -10) i (-15,18 / -10). Els punts d’intersecció de la paràbola amb l’eix X tenen coordenades (-1,318,0) i (1,518,0).
     • En el nostre exemple, les equacions de la forma estàndard 2x + 16x + 39:
     • x = (-16 +/- √ (16 - 4 (2) (39))) / 2 (2)
     • x = (-16 +/- √ (256 - 312)) / 4
     • x = (-16 +/- √ (-56) / - 10
     • Com que és impossible extreure l’arrel quadrada d’un nombre negatiu, en aquest cas la paràbola no talla l’eix X.
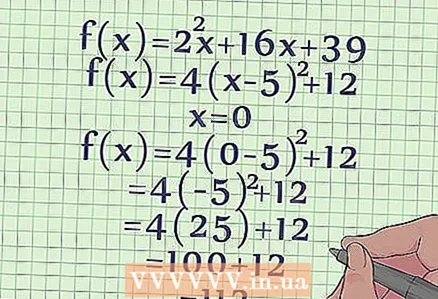9. 9 Localitzeu i dibuixeu la intercepció en Y segons calgui. És molt fàcil: connecteu x = 0 a l'equació original i cerqueu el valor de "y". La intercepció en Y sempre és la mateixa. Nota: a les equacions de la forma estàndard, el punt d'intersecció té coordenades (0, s).
   • Per exemple, la paràbola de l'equació quadràtica 2x + 16x + 39 es creua amb l'eix Y en el punt amb coordenades (0, 39), ja que c = 39. Però això es pot calcular:
     • f (x) = 2x + 16x + 39
     • f (x) = 2 (0) + 16 (0) + 39
     • f (x) = 39, és a dir, la paràbola d'aquesta equació quadràtica talla l'eix Y en el punt amb les coordenades (0, 39).
   • En el nostre exemple d’una equació no estàndard 4 (x - 5) + 12, la intercepció en y es calcula de la següent manera:
     • f (x) = 4 (x - 5) + 12
     • f (x) = 4 (0 - 5) + 12
     • f (x) = 4 (-5) + 12
     • f (x) = 4 (25) + 12
     • f (x) = 112, és a dir, la paràbola d’aquesta equació de segon grau talla l’eix Y en el punt amb les coordenades (0, 112).
10. 10 Heu trobat (i dibuixat) el vèrtex de la paràbola, la seva direcció i els punts d’intersecció amb els eixos X i Y. Podeu construir paràboles a partir d'aquests punts o trobar i traçar punts addicionals i només després construir una paràbola. Per fer-ho, connecteu diversos valors x (a banda i banda del vèrtex) a l'equació original per calcular els valors y corresponents.
    • Tornem a l'equació x + 2x + 1. Ja sabeu que el punt d'intersecció de la gràfica d'aquesta equació amb l'eix X és el punt amb coordenades (-1,0). Si la paràbola només té un punt d'intersecció amb l'eix X, aquest és el vèrtex de la paràbola situat a l'eix X. En aquest cas, un punt no és suficient per construir una paràbola regular. Així que trobeu alguns punts addicionals.
      • Diguem x = 0, x = 1, x = -2, x = -3.
      • x = 0: f (x) = (0) + 2 (0) + 1 = 1. Coordenades puntuals: (0,1).
      • x = 1: f (x) = (1) + 2 (1) + 1 = 4. Coordenades puntuals: (1,4).
      • x = -2: f (x) = (-2) + 2 (-2) + 1 = 1. Coordenades puntuals: (-2,1).
      • x = -3: f (x) = (-3) + 2 (-3) + 1 = 4. Coordenades puntuals: (-3,4).
      • Dibuixa aquests punts al pla de coordenades i dibuixa una paràbola (connecta els punts amb una corba en U). Tingueu en compte que la paràbola és absolutament simètrica: qualsevol punt d’una branca de la paràbola es pot reflectir (en relació amb l’eix de simetria) a l’altra branca de la paràbola. Això us estalviarà temps, ja que no cal calcular les coordenades dels punts de les dues branques de la paràbola.

Consells

• Arrodoneix els nombres fraccionats (si aquest és un requisit del professor): així es construeix una paràbola correcta.
• Si a f (x) = ax + bx + c els coeficients b o c són iguals a zero, no hi ha termes amb aquests coeficients a l’equació.Per exemple, 12x + 0x + 6 es converteix en 12x + 6 perquè 0x és 0.