Content

• Passos
• Mètode 1 de 3: Com resoldre una equació cúbica sense terme constant
• Mètode 2 de 3: Com trobar arrels senceres mitjançant multiplicadors
• Mètode 3 de 3: Com resoldre una equació mitjançant el discriminant

En una equació cúbica, l’exponent màxim és 3, tal equació té 3 arrels (solucions) i té la forma ${ displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0}$... Algunes equacions cúbiques no són tan fàcils de resoldre, però si apliqueu el mètode correcte (amb un bon antecedent teòric), podeu trobar les arrels fins i tot de l’equació cúbica més complexa; per a això, utilitzeu la fórmula per resoldre l’equació quadràtica. arrels senceres o calculeu el discriminant.

Passos

Mètode 1 de 3: Com resoldre una equació cúbica sense terme constant

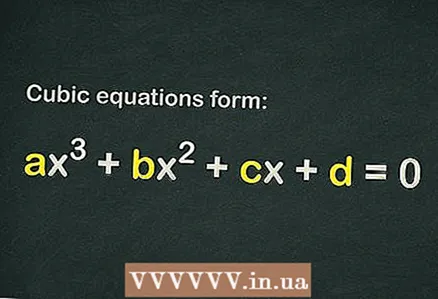1. 1 Esbrineu si hi ha un terme lliure a l’equació cúbica d{ displaystyle d}. L’equació cúbica té la forma ${ displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0}$... Perquè una equació es consideri cúbica, n’hi ha prou amb fer servir només el terme ${ displaystyle x ^ {3}}$ (és a dir, és possible que no hi hagi cap altre membre).
   • Si l’equació té un terme lliure ${ displaystyle d}$, utilitzeu un mètode diferent.
   • Si a l’equació ${ displaystyle a = 0}$, no és cúbic.
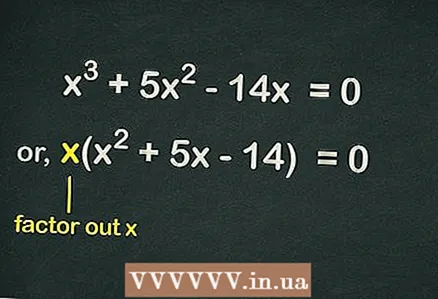2. 2 Traieu dels claudàtors x{ displaystyle x}. Com que no hi ha cap terme lliure a l'equació, cada terme de l'equació inclou la variable ${ displaystyle x}$... Això significa que aquell ${ displaystyle x}$ es pot excloure de parèntesis per simplificar l'equació. Per tant, l’equació s’escriurà així: ${ displaystyle x (ax ^ {2} + bx + c)}$.
   • Per exemple, donada una equació cúbica ${ displaystyle 3x ^ {3} -2x ^ {2} + 14x = 0}$
   • Per emportar ${ displaystyle x}$ claudàtors i obtenir ${ displaystyle x (3x ^ {2} -2x + 14) = 0}$
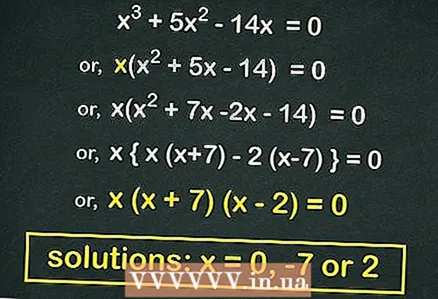3. 3 Factoreu (el producte de dos binomis) l’equació de segon grau (si és possible). Moltes equacions quadràtiques de la forma ${ displaystyle ax ^ {2} + bx + c = 0}$ es pot factoritzar. Tal equació resultarà si la traiem ${ displaystyle x}$ fora dels claudàtors. En el nostre exemple:
   • Traieu dels claudàtors ${ displaystyle x}$: ${ displaystyle x (x ^ {2} + 5x-14) = 0}$
   • Tingueu en compte l’equació de segon grau: ${ displaystyle x (x + 7) (x-2) = 0}$
   • Equivaleu cada paperera amb ${ displaystyle 0}$... Les arrels d’aquesta equació són ${ displaystyle x = 0, x = -7, x = 2}$.
4. 4 Resol una equació de segon grau mitjançant una fórmula especial. Feu això si l'equació de segon grau no es pot factoritzar. Per trobar dues arrels d’una equació, els valors dels coeficients ${ displaystyle a}$, ${ displaystyle b}$, ${ displaystyle c}$ substituir a la fórmula ${ displaystyle { frac {-b pm { sqrt {b ^ {2} -4ac}}} {2a}}}$.
   • En el nostre exemple, substituïu els valors dels coeficients ${ displaystyle a}$, ${ displaystyle b}$, ${ displaystyle c}$ (${ displaystyle 3}$, ${ displaystyle -2}$, ${ displaystyle 14}$) a la fórmula:

     ${ displaystyle { frac {-b pm { sqrt {b ^ {2} -4ac}}} {2a}}}$

     ${ displaystyle { frac {- (- 2) pm { sqrt {((-2) ^ {2} -4 (3) (14)}}} {2 (3)}}}$

     ${ displaystyle { frac {2 pm { sqrt {4- (12) (14)}}} {6}}}$

     ${ displaystyle { frac {2 pm { sqrt {(4-168}}} {6}}}$

     ${ displaystyle { frac {2 pm { sqrt {-164}}} {6}}}$

   • Primera arrel:

     ${ displaystyle { frac {2 + { sqrt {-164}}} {6}}}$

     ${ displaystyle { frac {2 + 12,8i} {6}}}$

   • Segona arrel:

     ${ displaystyle { frac {2-12,8i} {6}}}$

5. 5 Utilitzeu arrels quadràtiques i zero com a solucions a l’equació cúbica. Les equacions quadràtiques tenen dues arrels, mentre que les cúbiques en tenen tres. Ja heu trobat dues solucions: aquestes són les arrels de l’equació de segon grau. Si col·loqueu "x" fora dels claudàtors, la tercera solució seria ${ displaystyle 0}$.
   • Si traieu "x" dels claudàtors, obtindreu ${ displaystyle x (ax ^ {2} + bx + c) = 0}$, és a dir, dos factors: ${ displaystyle x}$ i una equació quadràtica entre claudàtors. Si algun d’aquests factors ho és ${ displaystyle 0}$, tota l'equació també és igual a ${ displaystyle 0}$.
   • Així, dues arrels d’una equació de segon grau són solucions d’una equació cúbica. La tercera solució és ${ displaystyle x = 0}$.

Mètode 2 de 3: Com trobar arrels senceres mitjançant multiplicadors

1. 1 Assegureu-vos que hi hagi un terme lliure a l’equació cúbica d{ displaystyle d}. Si en una equació de la forma ${ displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0}$ hi ha un membre gratuït ${ displaystyle d}$ (que no és igual a zero), no funcionarà posar "x" fora dels claudàtors. En aquest cas, utilitzeu el mètode descrit en aquesta secció.
   • Per exemple, donada una equació cúbica ${ displaystyle 2x ^ {3} + 9x ^ {2} + 13x = -6}$... Afegiu el zero a la part dreta de l'equació ${ displaystyle 6}$ als dos costats de l'equació.
   • L’equació resultarà ${ displaystyle 2x ^ {3} + 9x ^ {2} + 13x + 6 = 0}$... Com ${ displaystyle d = 6}$, no es pot utilitzar el mètode descrit a la primera secció.
2. 2 Anoteu els factors del coeficient a{ displaystyle a} i un membre lliure d{ displaystyle d}. És a dir, trobeu els factors del nombre a ${ displaystyle x ^ {3}}$ i números abans del signe igual. Recordem que els factors d’un nombre són els nombres que, multiplicats, produeixen aquest nombre.
   • Per exemple, per obtenir el número 6, cal multiplicar-se ${ displaystyle 6 times 1}$ i ${ displaystyle 2 times 3}$... Així doncs, els números 1, 2, 3, 6 són factors del nombre 6.
   • A la nostra equació ${ displaystyle a = 2}$ i ${ displaystyle d = 6}$... Multiplicadors 2 són 1 i 2... Multiplicadors 6 són els números 1, 2, 3 i 6.
3. 3 Dividiu cada factor a{ displaystyle a} per a cada factor d{ displaystyle d}. Com a resultat, obteniu moltes fraccions i diversos enters; les arrels de l’equació cúbica seran un dels enters o el valor negatiu d’un dels enters.
   • En el nostre exemple, divideix els factors ${ displaystyle a}$ (1 i 2) per factors ${ displaystyle d}$ (1, 2, 3 i 6). Obtindreu: ${ displaystyle 1}$, ${ displaystyle { frac {1} {2}}}$, ${ displaystyle { frac {1} {3}}}$, ${ displaystyle { frac {1} {6}}}$, ${ displaystyle 2}$ i ${ displaystyle { frac {2} {3}}}$... Ara afegiu valors negatius de les fraccions i nombres obtinguts a aquesta llista: ${ displaystyle 1}$, ${ displaystyle -1}$, ${ displaystyle { frac {1} {2}}}$, ${ displaystyle - { frac {1} {2}}}$, ${ displaystyle { frac {1} {3}}}$, ${ displaystyle - { frac {1} {3}}}$, ${ displaystyle { frac {1} {6}}}$, ${ displaystyle - { frac {1} {6}}}$, ${ displaystyle 2}$, ${ displaystyle -2}$, ${ displaystyle { frac {2} {3}}}$ i ${ displaystyle - { frac {2} {3}}}$... Totes les arrels de l’equació cúbica són alguns números d’aquesta llista.
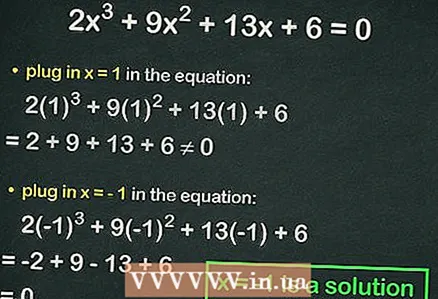4. 4 Connecteu els enters a l’equació cúbica. Si la igualtat és certa, el nombre substituït és l'arrel de l'equació. Per exemple, substituïu a l'equació ${ displaystyle 1}$:
   • ${ displaystyle 2 (1) ^ {3} +9 (1) ^ {2} +13 (1) +6}$ = ${ displaystyle 2 + 9 + 13 + 6}$ ≠ 0, és a dir, no s’observa la igualtat. En aquest cas, connecteu el número següent.
   • Suplent ${ displaystyle -1}$: ${ displaystyle (-2) +9 + (- 13) +6}$ = 0. Per tant, ${ displaystyle -1}$ és tota l'arrel de l'equació.
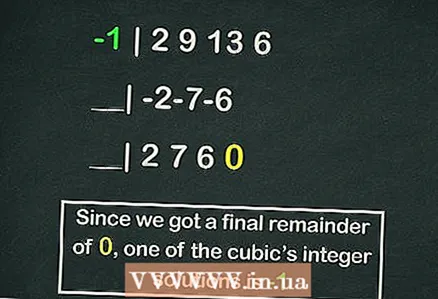5. 5 Utilitzeu el mètode de dividir polinomis per Esquema de Hornerper trobar les arrels de l’equació més ràpidament. Feu això si no voleu substituir manualment els números a l'equació. En l'esquema de Horner, els enters es divideixen entre els valors dels coeficients de l'equació ${ displaystyle a}$, ${ displaystyle b}$, ${ displaystyle c}$ i ${ displaystyle d}$... Si els nombres són divisibles de manera uniforme (és a dir, la resta és ${ displaystyle 0}$), un nombre enter és l'arrel de l'equació.
   • L’esquema de Horner mereix un article a part, però el següent és un exemple de càlcul d’una de les arrels de la nostra equació cúbica mitjançant aquest esquema:

     -1 | 2 9 13 6

     __| -2-7-6

     __| 2 7 6 0

   • Així que la resta és ${ displaystyle 0}$, però ${ displaystyle -1}$ és una de les arrels de l'equació.

Mètode 3 de 3: Com resoldre una equació mitjançant el discriminant

1. 1 Anoteu els valors dels coeficients de l’equació a{ displaystyle a}, b{ displaystyle b}, c{ displaystyle c} i d{ displaystyle d}. Us recomanem que escriviu prèviament els valors dels coeficients indicats per no confondre’s en el futur.
   • Per exemple, donada l’equació ${ displaystyle x ^ {3} -3x ^ {2} + 3x-1}$... Escriu a sota ${ displaystyle a = 1}$, ${ displaystyle b = -3}$, ${ displaystyle c = 3}$ i ${ displaystyle d = -1}$... Recordem que si abans ${ displaystyle x}$ no hi ha cap número, el coeficient corresponent encara existeix i és igual a ${ displaystyle 1}$.
2. 2 Calculeu el discriminant zero mitjançant una fórmula especial. Per resoldre una equació cúbica utilitzant el discriminant, heu de realitzar diversos càlculs difícils, però si realitzeu tots els passos correctament, aquest mètode esdevindrà indispensable per resoldre les equacions cúbiques més complexes. Primer càlcul ${ displaystyle Delta _ {0}}$ (zero discriminant) és el primer valor que necessitem; per fer-ho, substituïu els valors corresponents a la fórmula ${ displaystyle Delta _ {0} = b ^ {2} -3ac}$.
   • El discriminant és un nombre que caracteritza les arrels d’un polinomi (per exemple, el discriminant d’una equació de segon grau es calcula mitjançant la fórmula ${ displaystyle b ^ {2} -4ac}$).
   • A la nostra equació:

     ${ displaystyle b ^ {2} -3ac}$

     ${ displaystyle (-3) ^ {2} -3 (1) (3)}$

     ${ displaystyle 9-3 (1) (3)}$

     ${ displaystyle 9-9 = 0 = Delta _ {0}}$

3. 3 Calculeu el primer discriminant mitjançant la fórmula Δ1=2b3−9abc+27a2d{ displaystyle Delta _ {1} = 2b ^ {3} -9abc + 27a ^ {2} d}. Primer discriminant ${ displaystyle Delta _ {1}}$ - aquest és el segon valor important; per calcular-lo, connecteu els valors corresponents a la fórmula especificada.
   • A la nostra equació:

     ${ displaystyle 2 (-3) ^ {3} -9 (1) (- 3) (3) +27 (1) ^ {2} (- 1)}$

     ${ displaystyle 2 (-27) -9 (-9) +27 (-1)}$

     ${ displaystyle -54 + 81-27}$

     ${ displaystyle 81-81 = 0 = Delta _ {1}}$

4. 4 Calcular:${ displaystyle Delta = ( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) div -27a ^ {2}}$... És a dir, trobeu el discriminant de l’equació cúbica a través dels valors obtinguts ${ displaystyle Delta _ {0}}$ i ${ displaystyle Delta _ {1}}$... Si el discriminant d'una equació cúbica és positiu, l'equació té tres arrels; si el discriminant és zero, l'equació té una o dues arrels; si el discriminant és negatiu, l'equació té una arrel.
   • Una equació cúbica sempre té almenys una arrel, ja que la gràfica d'aquesta equació talla l'eix X almenys en un punt.
   • A la nostra equació ${ displaystyle Delta _ {0}}$ i ${ displaystyle Delta _ {1}}$ són iguals ${ displaystyle 0}$, de manera que podeu calcular fàcilment ${ displaystyle Delta}$:

     ${ displaystyle ( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) div (-27a ^ {2})}$

     ${ displaystyle ((0) ^ {2} -4 (0) ^ {3}) div (-27 (1) ^ {2})}$

     ${ displaystyle 0-0 div 27}$

     ${ displaystyle 0 = Delta}$... Per tant, la nostra equació té una o dues arrels.

5. 5 Calcular:${ displaystyle C = ^ {3} { sqrt { left ({ sqrt { Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}}} + Delta _ {1 } right) div 2}}}$. ${ displaystyle C}$ - aquesta és l'última quantitat important que es troba; us ajudarà a calcular les arrels de l’equació. Substituïu els valors per la fórmula especificada ${ displaystyle Delta _ {1}}$ i ${ displaystyle Delta _ {0}}$.
   • A la nostra equació:

     ${ displaystyle ^ {3} { sqrt {{ sqrt {( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) + Delta _ {1}}} div 2}}}$

     ${ displaystyle ^ {3} { sqrt {{ sqrt {(0 ^ {2} -4 (0) ^ {3}) + (0)}} div 2}}}$

     ${ displaystyle ^ {3} { sqrt {{ sqrt {(0-0) +0}} div 2}}}$

     ${ displaystyle 0 = C}$

6. 6 Troba tres arrels de l’equació. Feu-ho amb la fórmula ${ displaystyle - (b + u ^ {n} C + Delta _ {0} div (u ^ {n} C)) div 3a}$, on ${ displaystyle u = (- 1 + { sqrt {-3}}) div 2}$, però n és igual a 1, 2 o bé 3... Substituïu els valors adequats en aquesta fórmula; com a resultat, obtindreu tres arrels de l'equació.
   • Calculeu el valor mitjançant la fórmula a n = 1, 2 o bé 3i després comproveu la resposta. Si obteniu 0 quan comproveu la resposta, aquest valor és l'arrel de l'equació.
   • En el nostre exemple, substitueix 1 dins ${ displaystyle x ^ {3} -3x ^ {2} + 3x-1}$ i aconseguir 0, és a dir, 1 és una de les arrels de l'equació.