Com aplicar la transformada de Laplace a una funció

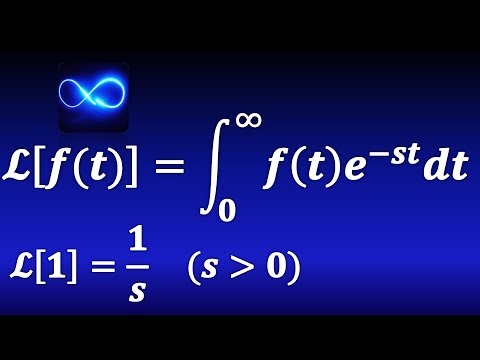
Vídeo: 168. Transformada de Laplace: ¿qué es?. Definición, explicación y primer ejemplo.

Content

Informació preliminar
Passos
Primera part de 3: els fonaments
Part 2 de 3: Propietats de la transformada de Laplace
Part 3 de 3: Trobar la transformada de Laplace per expansió de sèries

La transformada de Laplace és una transformada integral que s’utilitza per resoldre equacions diferencials amb coeficients constants. Aquesta transformació s’utilitza àmpliament en física i enginyeria.

Tot i que podeu utilitzar les taules adequades, és útil entendre la transformada de Laplace perquè pugueu fer-ho vosaltres mateixos si cal.

Informació preliminar

Donada una funció f(t){ displaystyle f (t)}definit per t≥0.{ displaystyle t geq 0.} Llavors Transformada de Laplace funció f(t){ displaystyle f (t)} és la següent funció de cada valor s{ displaystyle s}, en què convergeix la integral:
- ${ displaystyle F (s) = { mathcal {L}} {f (t) } = int _ {0} ^ { infty} f (t) e ^ {- st} mathrm {d} t}$
La transformada de Laplace pren una funció des de la regió t (escala de temps) fins a la regió s (regió de transformació), on ${ displaystyle F (s)}$ és una funció complexa d'una variable complexa. Us permet moure la funció a una zona on es pugui trobar una solució més fàcilment.
Transformbviament, la transformada de Laplace és un operador lineal, de manera que si tractem d’una suma de termes, cada integral es pot calcular per separat.
- ${ displaystyle int _ {0} ^ { infty} [af (t) + bg (t)] e ^ {- st} mathrm {d} t = a int _ {0} ^ { infty} f (t) e ^ {- st} mathrm {d} t + b int _ {0} ^ { infty} g (t) e ^ {- st} mathrm {d} t}$
Recordeu que la transformada de Laplace només funciona si convergeix la integral. Si la funció ${ displaystyle f (t)}$ té discontinuïtats, cal anar amb compte i fixar correctament els límits d’integració per evitar incerteses.

Passos

Primera part de 3: els fonaments

1 Substituïu la funció per la fórmula de la transformada de Laplace. Teòricament, la transformada de Laplace d'una funció és molt fàcil de calcular. Com a exemple, tingueu en compte la funció f(t)=eat{ displaystyle f (t) = e ^ {a}}, on a{ displaystyle a} és una constant complexa amb Re⁡(s)Re⁡(a).{ displaystyle operatorname {Re} (s) operatorname {Re} (a).}
- ${ displaystyle { mathcal {L}} {e ^ {at} } = int _ {0} ^ { infty} e ^ {at} e ^ {- st} mathrm {d} t}$
2 Valoreu la integral mitjançant els mètodes disponibles. En el nostre exemple, l'estimació és molt senzilla i podeu fer-ho amb càlculs senzills. En casos més complexos, poden ser necessaris mètodes més complexos, per exemple, la integració per parts o la diferenciació sota el signe integral. Condició de restricció Re⁡(s)Re⁡(a){ displaystyle operatorname {Re} (s) operatorname {Re} (a)} significa que la integral convergeix, és a dir, el seu valor tendeix a 0 com t→∞.{ displaystyle t to infty.}
- ${ displaystyle { begin {align} { mathcal {L}} {e ^ {at} } & = int _ {0} ^ { infty} e ^ {(as) t} mathrm {d } t & = { frac {e ^ {(as) t}} {as}} Bigg _ {0} ^ { infty} & = { frac {1} {sa}} end {alineat}}}$
- Tingueu en compte que això ens proporciona dos tipus de transformada de Laplace, amb sinus i cosinus, ja que segons la fórmula d'Euler ejoat{ displaystyle e ^ {iat}}... En aquest cas, en el denominador obtenim s−joa,{ displaystyle s-ia,} i només queda determinar les parts reals i imaginàries. També podeu avaluar el resultat directament, però això trigaria una mica més.
  - ${ displaystyle { mathcal {L}} { cos at } = operatorname {Re} left ({ frac {1} {s-ia}} right) = { frac {s} {s ^ {2} + a ^ {2}}}}$
  - ${ displaystyle { mathcal {L}} { sin at } = operatorname {Im} left ({ frac {1} {s-ia}} right) = { frac {a} {s ^ {2} + a ^ {2}}}}$
3 Penseu en la transformada de Laplace d'una funció de potència. En primer lloc, heu de definir la transformació de la funció de potència, ja que la propietat de linealitat us permet trobar la transformació per a de tots polinomis. Una funció de la forma tn,{ displaystyle t ^ {n},} on n{ displaystyle n} - qualsevol enter positiu. Es pot integrar peça per peça per definir una regla recursiva.
- ${ displaystyle { mathcal {L}} {t ^ {n} } = int _ {0} ^ { infty} t ^ {n} e ^ {- st} mathrm {d} t = { frac {n} {s}} { mathcal {L}} {t ^ {n-1} }}$
- Aquest resultat s’expressa de manera implícita, però si substituïu diversos valors n,{ displaystyle n,} podeu establir un patró determinat (proveu de fer-ho vosaltres mateixos), que us permet obtenir el resultat següent:
  - ${ displaystyle { mathcal {L}} {t ^ {n} } = { frac {n!} {s ^ {n + 1}}}}$
- També podeu definir la transformada de Laplace de potències fraccionàries mitjançant la funció gamma. Per exemple, d'aquesta manera es pot trobar la transformació d'una funció com f(t)=t.{ displaystyle f (t) = { sqrt {t}}.}
  - ${ displaystyle { mathcal {L}} {t ^ {n} } = { frac { Gamma (n + 1)} {s ^ {n + 1}}}}$
  - ${ displaystyle { mathcal {L}} {t ^ {1/2} } = { frac { Gamma (3/2)} {s ^ {3/2}}} = { frac { sqrt { pi}} {2s { sqrt {s}}}}}$
- Tot i que les funcions amb potències fraccionàries han de tenir talls (recordeu, qualsevol nombre complex ${ displaystyle z}$ i ${ displaystyle alpha}$ es pot escriure com ${ displaystyle z ^ { alpha}}$ , perquè el ${ displaystyle e ^ { alpha operatorname {Log} z}}$ ), sempre es poden definir de manera que els talls es trobin al mig pla esquerre i així evitar problemes d’analítica.

Part 2 de 3: Propietats de la transformada de Laplace

1 Trobem la transformada de Laplace de la funció multiplicada per eat{ displaystyle e ^ {at}}. Els resultats obtinguts a la secció anterior ens van permetre conèixer algunes propietats interessants de la transformada de Laplace. La transformada de Laplace de funcions com el cosinus, el sinus i la funció exponencial sembla ser més senzilla que la transformada de la funció de potència. Multiplicació per eat{ displaystyle e ^ {at}} a la regió t correspon a torn a la regió s:
- ${ displaystyle { mathcal {L}} {e ^ {at} f (t) } = int _ {0} ^ { infty} f (t) e ^ {- (sa) t} mathrm {d} t = F (sa)}$
- Aquesta propietat us permet trobar immediatament la transformació de funcions com f(t)=e3tpecat⁡2t{ displaystyle f (t) = e ^ {3t} sin 2t}, sense haver de calcular la integral:
  - ${ displaystyle { mathcal {L}} {e ^ {3t} sin 2t } = { frac {2} {(s-3) ^ {2} +4}}}$
2 Trobem la transformada de Laplace de la funció multiplicada per tn{ displaystyle t ^ {n}}. En primer lloc, considereu la multiplicació per t{ displaystyle t}... Per definició, es pot diferenciar una funció per una integral i obtenir un resultat sorprenentment senzill:
- ${ displaystyle { begin {align} { mathcal {L}} {tf (t) } & = int _ {0} ^ { infty} tf (t) e ^ {- st} mathrm { d} t & = - int _ {0} ^ { infty} f (t) { frac { partial} { partial s}} e ^ {- st} mathrm {d} t & = - { frac { mathrm {d}} { mathrm {d} s}} int _ {0} ^ { infty} f (t) e ^ {- st} mathrm {d} t & = - { frac { mathrm {d} F} { mathrm {d} s}} end {align}}}$
- Repetint aquesta operació, obtenim el resultat final:
  - ${ displaystyle { mathcal {L}} {t ^ {n} f (t) } = (- 1) ^ {n} { frac { mathrm {d} ^ {n} F} { mathrm {d} s ^ {n}}}}$
- Tot i que la reordenació dels operadors d’integració i diferenciació requereix una justificació addicional, no la presentarem aquí, sinó que només tinguem en compte que aquesta operació és correcta si el resultat final té sentit. També es pot tenir en compte el fet que les variables ${ displaystyle s}$ i ${ displaystyle t}$ no depenen els uns dels altres.
- Mitjançant aquesta regla, és fàcil trobar la transformació de funcions com t2cos⁡2t{ displaystyle t ^ {2} cos 2t}, sense reintegrar per parts:
  - ${ displaystyle { mathcal {L}} {t ^ {2} cos 2t } = { frac { mathrm {d} ^ {2}} { mathrm {d} s ^ {2}}} { frac {s} {s ^ {2} +4}} = { frac {2s ^ {3} -24s} {(s ^ {2} +4) ^ {3}}}}$
3 Trobeu la transformada de Laplace de la funció f(at){ displaystyle f (at)}. Això es pot fer fàcilment substituint la variable per u mitjançant la definició d'una transformada:
- ${ displaystyle { begin {align} { mathcal {L}} {f (at) } & = int _ {0} ^ { infty} f (at) e ^ {- st} mathrm { d} t, u = at & = { frac {1} {a}} int _ {0} ^ { infty} f (u) e ^ {- su / a} mathrm {d } u & = { frac {1} {a}} F left ({ frac {s} {a}} right) end {align}}}$
- A la part superior, hem trobat la transformada de funcions de Laplace ${ displaystyle sin at}$ i ${ displaystyle cos at}$ directament des de la funció exponencial. Utilitzant aquesta propietat, podeu obtenir el mateix resultat si trobeu les parts reals i imaginàries ${ displaystyle { mathcal {L}} {e ^ {it} } = { frac {1} {s-i}}}$ .
4 Trobeu la transformada de Laplace de la derivada f′(t){ displaystyle f ^ { prime} (t)}. A diferència dels exemples anteriors, en aquest cas haver de integrar peça per peça:
- ${ displaystyle { begin {align} { mathcal {L}} {f ^ { prime} (t) } & = int _ {0} ^ { infty} f ^ { prime} (t ) e ^ {- st} mathrm {d} t, u = e ^ {- st}, mathrm {d} v = f ^ { prime} (t) mathrm {d} t & = f (t) e ^ {- st} Big _ {0} ^ { infty} + s int _ {0} ^ { infty} f (t) e ^ {- st} mathrm {d } t & = sF (s) -f (0) end {align}}}$
- Com que la segona derivada es produeix en molts problemes físics, també trobem la transformada de Laplace:
  - ${ displaystyle { mathcal {L}} {f ^ { prime prime} (t) } = s ^ {2} F (s) -sf (0) -f ^ { prime} (0) }$
- En el cas general, la transformada de Laplace de la derivada de novè ordre es defineix de la següent manera (això permet resoldre equacions diferencials mitjançant la transformada de Laplace):
  - ${ displaystyle { mathcal {L}} {f ^ {(n)} (t) } = s ^ {n} F (s) - sum _ {k = 0} ^ {n-1} s ^ {nk-1} f ^ {(k)} (0)}$

Part 3 de 3: Trobar la transformada de Laplace per expansió de sèries

1 Trobem la transformada de Laplace per a una funció periòdica. La funció periòdica compleix la condició f(t)=f(t+nT),{ displaystyle f (t) = f (t + nT),} on T{ displaystyle T} és el període de la funció, i n{ displaystyle n} és un nombre enter positiu. Les funcions periòdiques s’utilitzen àmpliament en moltes aplicacions, inclosos el processament de senyals i l’enginyeria elèctrica. Mitjançant transformacions simples, obtenim el següent resultat:
- ${ displaystyle { begin {align} { mathcal {L}} {f (t) } & = int _ {0} ^ { infty} f (t) e ^ {- st} mathrm { d} t & = sum _ {n = 0} ^ { infty} int _ {nT} ^ {(n + 1) T} f (t) e ^ {- st} mathrm {d} t & = sum _ {n = 0} ^ { infty} int _ {0} ^ {T} f (t + nT) e ^ {- s (t + nT)} mathrm {d} t & = sum _ {n = 0} ^ { infty} e ^ {- snT} int _ {0} ^ {T} f (t) e ^ {- st} mathrm {d} t & = { frac {1} {1-e ^ {- sT}}} int _ {0} ^ {T} f (t) e ^ {- st} mathrm {d} t end { alineats}}}$
- Com podeu veure, en el cas d’una funció periòdica, és suficient realitzar la transformada de Laplace durant un període.
2 Realitzeu la transformada de Laplace per al logaritme natural. En aquest cas, la integral no es pot expressar en forma de funcions elementals. L’ús de la funció gamma i la seva expansió en sèrie permet estimar el logaritme natural i els seus graus. La presència de la constant d'Euler-Mascheroni γ{ displaystyle gamma} mostra que per estimar aquesta integral, cal utilitzar una expansió en sèrie.
- ${ displaystyle { mathcal {L}} { ln t } = - { frac { gamma + ln s} {s}}}$
3 Penseu en la transformada de Laplace de la funció sinc no normalitzada. Funció sinc⁡(t)=pecat⁡tt{ displaystyle operatorname {sinc} (t) = { frac { sin t} {t}}} àmpliament utilitzat per al processament de senyals, en equacions diferencials equival a la funció esfèrica de Bessel de primer ordre i zero j0(x).{ displaystyle j_ {0} (x).} La transformada de Laplace d'aquesta funció tampoc no es pot calcular mitjançant mètodes estàndard. En aquest cas, es realitza la transformació de membres individuals de la sèrie, que són funcions de potència, de manera que les seves transformacions necessàriament convergeixen en un interval determinat.
- En primer lloc, escrivim l'expansió de la funció en una sèrie de Taylor:
  - ${ displaystyle { frac { sin t} {t}} = sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n} t ^ {2n}} {(2n +1)!}}}$
- Ara fem servir la ja coneguda transformada de Laplace d'una funció de potència. Els factorials es cancel·len i, com a resultat, obtenim l'expansió de Taylor per a l'arcangent, és a dir, una sèrie alterna que s'assembla a la sèrie de Taylor per al sinus, però sense factorials:
  - ${ displaystyle { begin {align} { mathcal {L}} left {{ frac { sin t} {t}} right } & = sum _ {n = 0} ^ { infty } { frac {(-1) ^ {n} (2n)!} {(2n + 1)!}} { frac {1} {s ^ {2n + 1}}} & = sum _ {n = 0} ^ { infty} { frac {(-1) ^ {n}} {2n + 1}} { frac {1} {s ^ {2n + 1}}} & = tan ^ {- 1} { frac {1} {s}} end {align}}}$