Content

• Passos
• Consells

La funció racional té la forma y = N (x) / D (x), on N i D són polinomis. Per representar aquesta funció amb precisió, necessiteu un bon coneixement d’àlgebra, inclosos els càlculs diferencials. Penseu en el següent exemple: y = (2x - 6x + 5)/(4x + 2).

Passos

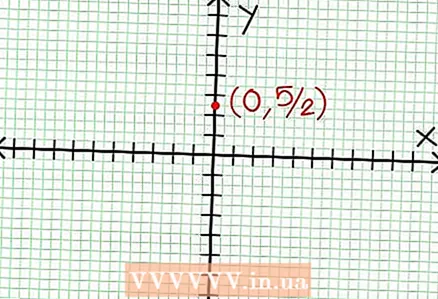1. 1 Trobeu la intersecció en y del gràfic. Per fer-ho, substituïu x = 0 per la funció i obteniu y = 5/2. Així, el punt d’intersecció del gràfic amb l’eix Y té coordenades (0, 5/2).Col·loqueu aquest punt al pla de coordenades.
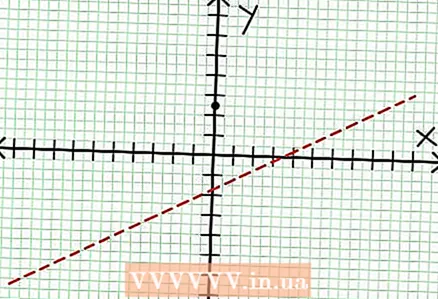2. 2 Cerqueu les asímptotes horitzontals. Dividiu el numerador pel denominador (en una columna) per determinar el comportament de "y" amb valors de "x" tendents a l'infinit. En el nostre exemple, la divisió serà y = (1/2)x - (7/4) + 17/(8x + 4). Per a valors positius o negatius grans de "x" 17 / (8x + 4) tendeix a zero i el gràfic s’acosta a la línia recta donada per la funció y = (1/2)x - (7/4). Mitjançant la línia de punts, traqueu aquesta funció.
   • Si el grau del numerador és inferior al grau del denominador, no podeu dividir el numerador pel denominador i l'asímptota es descriurà per la funció a = 0.
   • Si el grau del numerador és igual al grau del denominador, l'asímptota és una línia horitzontal igual a la proporció dels coeficients en "x" en el grau més alt.
   • Si el grau del numerador és 1 més que el grau del denominador, l'asímptota és una recta inclinada, el pendent de la qual és igual a la proporció dels coeficients de "x" al grau més alt.
   • Si el grau del numerador és superior al grau del denominador en 2, 3, etc., llavors per a valors grans |NS| significat a tendeixen a l'infinit (positiu o negatiu) en forma de quadrat, cúbic o un altre grau de polinomi. En aquest cas, molt probablement, no necessiteu crear una gràfica exacta de la funció obtinguda dividint el numerador pel denominador.
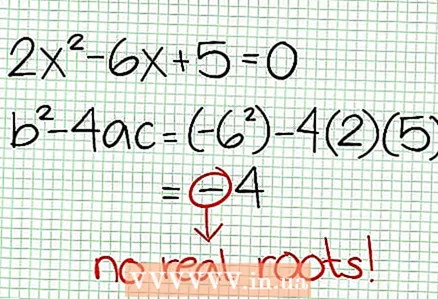3. 3 Cerqueu els zeros de la funció. Una funció racional té zeros quan el seu numerador és zero, és a dir, N (NS) = 0. En el nostre exemple, 2x - 6x + 5 = 0. El discriminant d'aquesta equació de segon grau: b - 4AC = 6 - 4 * 2 * 5 = 36 - 40 = -4. Com que el discriminant és negatiu, llavors N (NS) i, per tant, F (NS) no té arrels reals. El gràfic d’una funció racional no talla l’eix X. Si la funció té zeros (arrels), poseu-los al pla de coordenades.
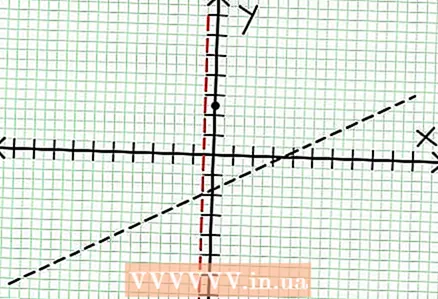4. 4 Cerqueu les assimptotes verticals. Per fer-ho, establiu el denominador a zero. En el nostre exemple, 4x + 2 = 0 i NS = -1/2. Representa l’asímptota vertical mitjançant la línia de punts. Si per algun valor NS N (NS) = 0 i D (NS) = 0, llavors l'asímptota vertical existeix o no (és un cas rar, però és millor recordar-ho).
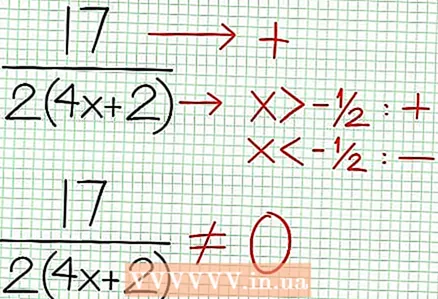5. 5 Mireu la resta del numerador dividit pel denominador. És positiu, negatiu o zero? En el nostre exemple, la resta és de 17, cosa positiva. Denominador 4x + 2 positius a la dreta de l'asímptota vertical i negatius a l'esquerra d'aquesta. Això significa que la gràfica de la funció racional per a valors positius grans NS s'aproxima a l'asímptota des de dalt i per a grans valors negatius NS - des de sota. Des del 17 / (8x + 4) no és mai igual a zero, aleshores la gràfica d'aquesta funció mai no tallarà la línia recta especificada per la funció a = (1/2)NS - (7/4).
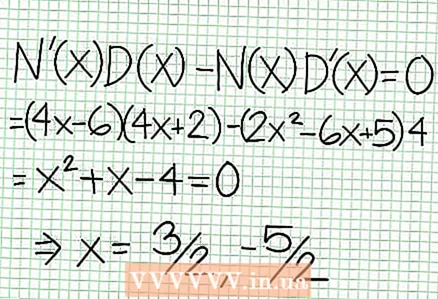6. 6 Cerqueu extremes locals. Existeix un extremum local per a N '(x) D (x) - N (x) D ’(x) = 0. En el nostre exemple, N ’(x) = 4x - 6 i D '(x) = 4. N ’(x) D (x) - N (x) D ’(x) = (4x - 6)(4x + 2) - (2x - 6x + 5)*4 = x + x - 4 = 0. Resolent aquesta equació, trobareu que x = 3/2 i x = -5/2. (No són valors del tot precisos, però són adequats per al nostre cas quan no cal superprecisió.)
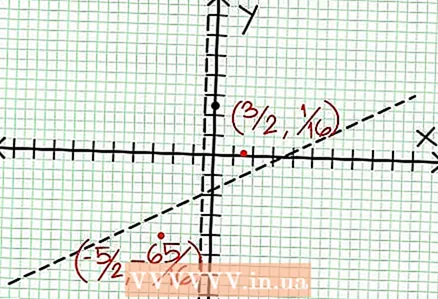7. 7 Cerqueu el valor a per a cada extremum local. Per fer-ho, substituïu els valors NS a la funció racional original. En el nostre exemple, f (3/2) = 1/16 i f (-5/2) = -65/16. Deixeu de banda els punts (3/2, 1/16) i (-5/2, -65/16) al pla de coordenades. Atès que els càlculs es basen en valors aproximats (del pas anterior), el mínim i el màxim trobats tampoc són del tot precisos (però probablement molt a prop dels valors exactes). (El punt (3/2, 1/16) és molt proper al mínim local. A partir del pas 3, ho sabem a sempre positiu per NS> -1/2 i hem trobat un valor petit (1/16); per tant, el valor d'error és extremadament petit en aquest cas.)
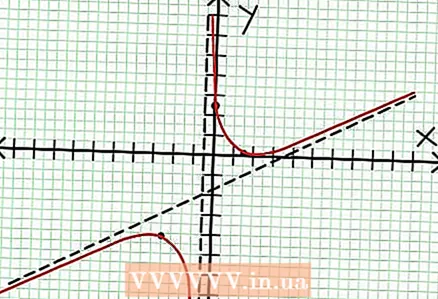8. 8 Connecteu els punts pendents i esteneu el gràfic sense problemes fins a les asímptotes (no us oblideu de la direcció correcta del gràfic que s’acosta a les asímptotes). Recordeu que el gràfic no ha de creuar l'eix X (vegeu el pas 3). El gràfic tampoc no es creua amb les asímptotes horitzontals i verticals (vegeu el pas 5). No canvieu la direcció del gràfic excepte en els punts extrems del pas anterior.

Consells

• Si heu seguit els passos anteriors estrictament en ordre, no cal que calculeu les segones derivades (o quantitats complexes similars) per provar la vostra solució.
• Si no necessiteu calcular els valors de les quantitats, podeu substituir la cerca d'extrems locals calculant alguns parells addicionals de coordenades (NS, a) entre cada parell d’asímptotes. A més, si no us interessa com funciona el mètode descrit, no us sorprengueu per què no podeu trobar la derivada i resoldre l'equació N '(x) D (x) - N (x) D ’(x) = 0.
• En alguns casos, haureu de treballar amb polinomis d’ordre superior. Si no podeu trobar la solució exacta mitjançant factorització, fórmules, etc., estimeu possibles solucions mitjançant mètodes numèrics com el mètode de Newton.
• En casos rars, el numerador i el denominador comparteixen un factor variable comú. Segons els passos descrits, això portarà a zero i a una asímptota vertical al mateix lloc. Tanmateix, això no és possible i l'explicació és una de les següents:
  • Zero en N (NS) té una multiplicitat superior a zero en D (NS). Gràfic F (NS) tendeix a zero en aquest moment, però no s’hi defineix. Indiqueu-ho dibuixant un cercle al voltant del punt.
  • Zero en N (NS) i zero en D (NS) tenen la mateixa multiplicitat. El gràfic s'aproxima a algun punt diferent de zero en aquest valor NSperò no s’hi defineix. Indiqueu-ho dibuixant un cercle al voltant del punt.
  • Zero en N (NS) té una multiplicitat inferior a zero en D (NS). Aquí hi ha una asimptota vertical.