Content

• Passos
• Mètode 1 de 3: primera part: determinar el punt d'inflexió
• Mètode 2 de 3: càlcul de les derivades d'una funció
• Mètode 3 de 3: Part 3: trobar el punt d'inflexió
• Consells

En el càlcul diferencial, un punt d'inflexió és un punt d'una corba en què la seva curvatura canvia de signe (de més a menys o de menys a més). Aquest concepte s’utilitza en enginyeria mecànica, economia i estadística per identificar canvis significatius en les dades.

Passos

Mètode 1 de 3: primera part: determinar el punt d'inflexió

1. 1 Definició d'una funció còncava. El centre de qualsevol acord (un segment que connecta dos punts) del gràfic d'una funció còncava es troba a sota del gràfic o bé sobre ell.
2. 2 Definició d'una funció convexa. El centre de qualsevol acord (un segment que connecta dos punts) del gràfic d'una funció convexa es troba a sobre del gràfic o bé sobre ell.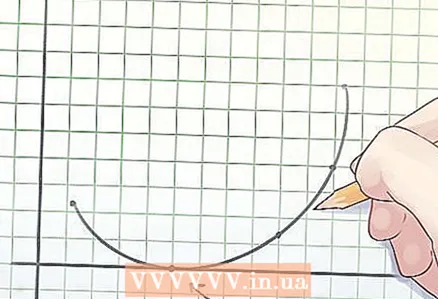
3. 3 Determinació de les arrels de la funció. L'arrel d'una funció és el valor de la variable "x" en què y = 0.
   • Quan es traça una funció, les arrels són els punts en què la gràfica creua l'eix x.

Mètode 2 de 3: càlcul de les derivades d'una funció

1. 1 Cerqueu la primera derivada de la funció. Mireu les regles de diferenciació al llibre de text; heu d’aprendre a prendre les primeres derivades i, tot seguit, passar a càlculs més complexos. Els primers derivats es designen f '(x). Per a expressions de la forma ax ^ p + bx ^ (p - 1) + cx + d, la primera derivada és: apx ^ (p - 1) + b (p - 1) x ^ (p - 2) + c.
   • Per exemple, trobeu els punts d'inflexió de la funció f (x) = x ^ 3 + 2x -1. La primera derivada d'aquesta funció és:
     
     f ′ (x) = (x ^ 3 + 2x - 1) ′ = (x ^ 3) ′ + (2x) ′ - (1) ′ = 3x ^ 2 + 2 + 0 = 3x2 + 2
2. 2 Troba la segona derivada de la funció. La segona derivada és la derivada de la primera derivada de la funció original. La segona derivada es denota com f ′ ′ (x).
   • A l'exemple anterior, la segona derivada és:
     
     f ′ ′ (x) = (3x2 + 2) ′ = 2 × 3 × x + 0 = 6x
3. 3 Estableix la segona derivada a zero i resol l’equació resultant. El resultat serà el punt d’inflexió previst.
   • A l'exemple anterior, el vostre càlcul té aquest aspecte:
     
     f ′ ′ (x) = 0
     6x = 0
     x = 0
4. 4 Troba la tercera derivada de la funció. Per verificar que el resultat sigui realment un punt d'inflexió, busqueu la tercera derivada, que és la derivada de la segona derivada de la funció original. La tercera derivada es denota com f ′ ′ ′ (x).
   • A l'exemple anterior, la tercera derivada és:
     
     f ′ ′ ′ (x) = (6x) ′ = 6

Mètode 3 de 3: Part 3: trobar el punt d'inflexió

1. 1 Consulteu la tercera derivada. La regla estàndard per estimar un punt d'inflexió és que si la tercera derivada no és nul·la (és a dir, f ′ ′ ′ (x) ≠ 0), el punt d'inflexió és el veritable punt d'inflexió. Consulteu la tercera derivada; si no és zero, heu trobat el punt d'inflexió real.
   • A l'exemple anterior, la tercera derivada és 6, no 0.Així que heu trobat el veritable punt d’inflexió.
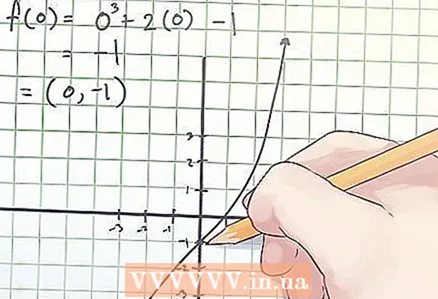2. 2 Cerqueu les coordenades del punt d’inflexió. Les coordenades del punt d'inflexió es denoten com (x, f (x)), on x és el valor de la variable independent "x" al punt d'inflexió, f (x) és el valor de la variable dependent "y" a la flexió punt.
   • A l'exemple anterior, quan s'equipara la segona derivada a zero, heu trobat que x = 0. Per tant, per determinar les coordenades del punt d'inflexió, trobeu f (0). El vostre càlcul té aquest aspecte:
     
     f (0) = 0 ^ 3 + 2 × 0−1 = −1.
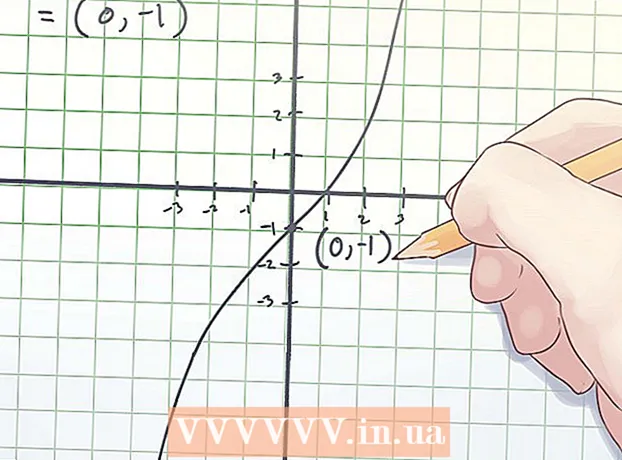
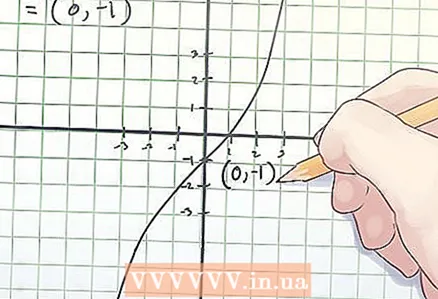3. 3 Anoteu les coordenades del punt d’inflexió. Les coordenades del punt d’inflexió són els valors x i f (x) trobats.
   • A l'exemple anterior, el punt d'inflexió es troba a les coordenades (0, -1).

Consells

• La primera derivada d’un terme lliure (nombre primer) sempre és zero.