Content

• Passos
• Mètode 1 de 4: Monomi al denominador
• Mètode 2 de 4: binomi en el denominador
• Mètode 3 de 4: expressió inversa
• Mètode 4 de 4: denominador d'arrel cúbica

En matemàtiques, no és habitual deixar una arrel o un nombre irracional en el denominador d’una fracció. Si el denominador és una arrel, multipliqueu la fracció per algun terme o expressió per eliminar l’arrel. Les calculadores modernes permeten treballar amb arrels al denominador, però el programa educatiu requereix que els estudiants puguin desfer-se de la irracionalitat del denominador.

Passos

Mètode 1 de 4: Monomi al denominador

1. 1 Aprèn la fracció. La fracció s’escriu correctament si no hi ha arrel al denominador. Si el denominador té un quadrat o qualsevol altra arrel, heu de multiplicar el numerador i el denominador per algun monomi per desfer-vos de l’arrel. Tingueu en compte que el numerador pot contenir una arrel; això és normal.
   • ${ displaystyle { frac {7 { sqrt {3}}} {2 { sqrt {7}}}}}$
   • El denominador aquí té una arrel ${ displaystyle { sqrt {7}}}$.
2. 2 Multiplicar el numerador i el denominador per l’arrel del denominador. Si el denominador conté un monomi, és molt fàcil racionalitzar aquesta fracció. Multiplicar el numerador i el denominador pel mateix monomi (és a dir, està multiplicant la fracció per 1).
   • ${ displaystyle { frac {7 { sqrt {3}}} {2 { sqrt {7}}}} cdot { frac { sqrt {7}} { sqrt {7}}}}$
   • Si introduïu una expressió per a una solució en una calculadora, assegureu-vos de posar parèntesis al voltant de cada part per separar-les.
3. 3 Simplifiqueu la fracció (si és possible). En el nostre exemple, es pot abreviar dividint el numerador i el denominador per 7.
   • ${ displaystyle { frac {7 { sqrt {3}}} {2 { sqrt {7}}}} cdot { frac { sqrt {7}} { sqrt {7}}} = { frac {7 { sqrt {21}}} {14}} = { frac { sqrt {21}} {2}}}$

Mètode 2 de 4: binomi en el denominador

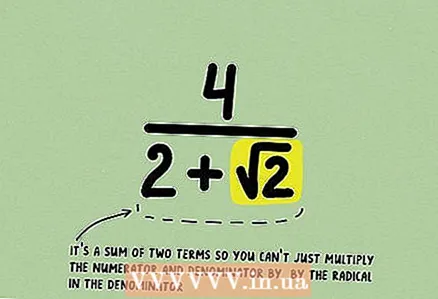1. 1 Aprèn la fracció. Si el seu denominador conté la suma o la diferència de dos monomis, un dels quals conté una arrel, és impossible multiplicar la fracció per aquest binomi per desfer-se de la irracionalitat.
   • ${ displaystyle { frac {4} {2 + { sqrt {2}}}}}$
   • Per entendre-ho, escriviu la fracció ${ displaystyle { frac {1} {a + b}}}$on el monomi ${ displaystyle a}$ o bé ${ displaystyle b}$ conté l'arrel. En aquest cas: ${ displaystyle (a + b) (a + b) = a ^ {2} + 2ab + b ^ {2}}$... Així, el monomi ${ displaystyle 2ab}$ encara inclourà l'arrel (si ${ displaystyle a}$ o bé ${ displaystyle b}$ conté l'arrel).
   • Vegem el nostre exemple.
     • ${ displaystyle { frac {4} {2 + { sqrt {2}}}} cdot { frac {2 + { sqrt {2}}} {2 + { sqrt {2}}}} = { frac {4 (2 + { sqrt {2}})} {4 + 4 { sqrt {2}} + 2}}}$
   • Veureu que no us podeu desfer del monomi del denominador ${ displaystyle 4 { sqrt {2}}}$.
2. 2 Multiplicar el numerador i el denominador pel binomi conjugat del binomi en el denominador. Un binomi conjugat és un binomi amb el mateix monomi, però amb el signe oposat entre ells. Per exemple, binom ${ displaystyle 2 + { sqrt {2}}}$ conjugat a un binomi ${ displaystyle 2 - { sqrt {2}}.}$
   • ${ displaystyle { frac {4} {2 + { sqrt {2}}}} cdot { frac {2 - { sqrt {2}}} {2 - { sqrt {2}}}}$
   • Comprendre el significat d’aquest mètode. Considereu la fracció de nou ${ displaystyle { frac {1} {a + b}}}$... Multiplicar el numerador i el denominador pel binomi conjugat al binomi del denominador: ${ displaystyle (a + b) (a-b) = a ^ {2} -b ^ {2}}$... Per tant, no hi ha monomis que continguin arrels. Des dels monomis ${ displaystyle a}$ i ${ displaystyle b}$ són quadrades, les arrels s’eliminaran.
3. 3 Simplifiqueu la fracció (si és possible). Si hi ha un factor comú tant al numerador com al denominador, cancel·leu-lo. En el nostre cas, 4 - 2 = 2, que es pot utilitzar per reduir la fracció.
   • ${ displaystyle { frac {4} {2 + { sqrt {2}}}} cdot { frac {2 - { sqrt {2}}} {2 - { sqrt {2}}}} = { frac {4 (2 - { sqrt {2}})} {4-2}} = 4-2 { sqrt {2}}}$

Mètode 3 de 4: expressió inversa

1. 1 Examineu el problema. Si necessiteu trobar una expressió que sigui inversa a la que conté una arrel, haureu de racionalitzar la fracció resultant (i només simplificar-la). En aquest cas, utilitzeu el mètode descrit a la primera o segona secció (segons la tasca).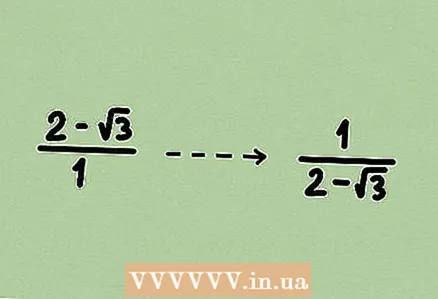
   • ${ displaystyle 2 - { sqrt {3}}}$
2. 2 Anota l’expressió contrària. Per fer-ho, divideix 1 per l’expressió donada; si es dóna una fracció, canvieu el numerador i el denominador. Recordeu que qualsevol expressió és una fracció amb 1 al denominador.
   • ${ displaystyle { frac {1} {2 - { sqrt {3}}}}}$
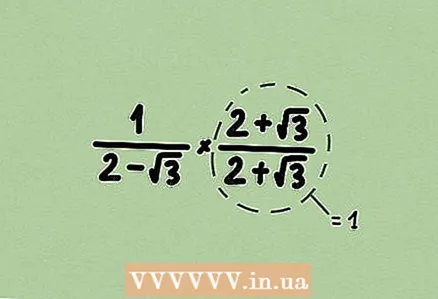3. 3 Multiplicar el numerador i el denominador per alguna expressió per desfer-se de l'arrel. En multiplicar el numerador i el denominador per la mateixa expressió, multiplicareu la fracció per 1, és a dir, el valor de la fracció no canvia. En el nostre exemple, se’ns dóna un binomi, de manera que multipliqueu el numerador i el denominador pel binomi conjugat.
   • ${ displaystyle { frac {1} {2 - { sqrt {3}}}} cdot { frac {2 + { sqrt {3}}} {2 + { sqrt {3}}}}}$
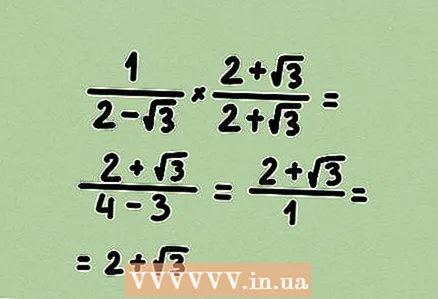4. 4 Simplifiqueu la fracció (si és possible). En el nostre exemple, 4 - 3 = 1, de manera que l’expressió del denominador de la fracció es pot cancel·lar completament.
   • ${ displaystyle { frac {1} {2 - { sqrt {3}}}} cdot { frac {2 + { sqrt {3}}} {2 + { sqrt {3}}}} = { frac {2 + { sqrt {3}}} {4-3}} = 2 + { sqrt {3}}}$
   • La resposta és un binomi conjugat a aquest binomi. És només una casualitat.

Mètode 4 de 4: denominador d'arrel cúbica

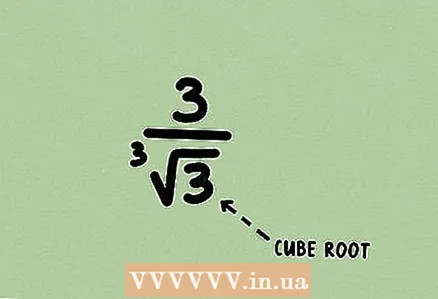1. 1 Aprèn la fracció. El problema pot contenir arrels cubes, tot i que és bastant rar. El mètode descrit és aplicable a arrels de qualsevol grau.
   • ${ displaystyle { frac {3} { sqrt [{3}] {3}}}}$
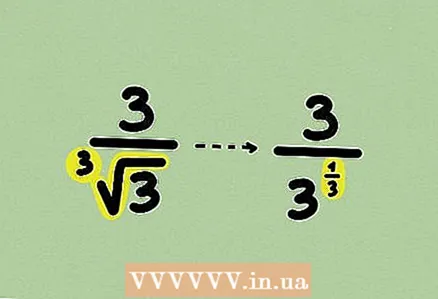2. 2 Torneu a escriure l'arrel com a potència. Aquí no es pot multiplicar el numerador i el denominador per algun monomi o expressió, perquè la racionalització es duu a terme d’una manera lleugerament diferent.
   • ${ displaystyle { frac {3} {3 ^ {1/3}}}}$
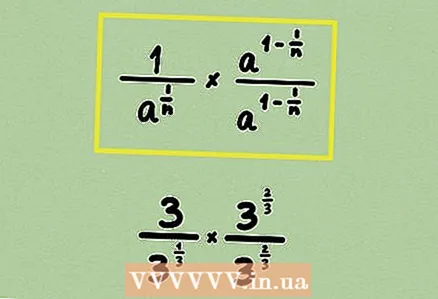3. 3 Multiplicar el numerador i el denominador de la fracció per alguna potència de manera que l’exponent del denominador es converteixi en 1. Al nostre exemple, multiplica la fracció per ${ displaystyle { frac {3 ^ {2/3}} {3 ^ {2/3}}}}$... Recordeu que quan es multipliquen els graus, els seus indicadors se sumen: ${ displaystyle a ^ {b} a ^ {c} = a ^ {b + c}.}$
   • ${ displaystyle { frac {3} {3 ^ {1/3}}} cdot { frac {3 ^ {2/3}} {3 ^ {2/3}}}}$
   • Aquest mètode és aplicable a qualsevol arrel de grau n. Si es dóna una fracció ${ displaystyle { frac {1} {a ^ {1 / n}}}}$, multipliqueu el numerador i el denominador per ${ displaystyle a ^ {1 - { frac {1} {n}}}}$... Així, l'exponent del denominador es converteix en 1.
4. 4 Simplifiqueu la fracció (si és possible).
   • ${ displaystyle { frac {3} {3 ^ {1/3}}} cdot { frac {3 ^ {2/3}} {3 ^ {2/3}}} = 3 ^ {2/3 }}$
   • Si cal, escriviu l'arrel a la resposta. En el nostre exemple, divideix l'exponent en dos factors: ${ displaystyle 1/3}$ i ${ displaystyle 2}$.
     • ${ displaystyle 3 ^ {2/3} = (3 ^ {2}) ^ {1/3} = { sqrt [{3}] {9}}}$