Content

• Per trepitjar
• Mètode 1 de 4: determinar el pes
• Mètode 2 de 4: determineu el punt zero
• Mètode 3 de 4: determinar el centre de gravetat
• Mètode 4 de 4: comproveu la vostra resposta
• Consells
• Advertiments

El centre de gravetat (el centre de massa) és el centre de la distribució del pes d’un objecte: el punt on la gravetat actua sobre aquest objecte. Aquest és el punt en què l’objecte es troba en perfecte equilibri, independentment de com l’objecte hagi girat o girat al voltant d’aquest punt. Si voleu saber calcular el centre de gravetat d’un objecte, necessiteu el pes de l’objecte i de tots els objectes que hi ha. A continuació, determineu un punt zero i processeu les magnituds conegudes a l’equació per calcular el centre de gravetat d’un objecte o sistema. Si voleu saber calcular el centre de gravetat, seguiu els passos següents.

Per trepitjar

Mètode 1 de 4: determinar el pes

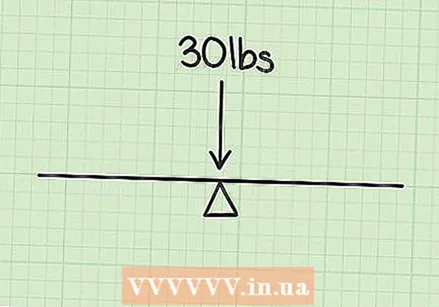1. Calculeu el pes de l'objecte. En calcular el centre de gravetat, primer haureu d’esbrinar el pes de l’objecte. Suposem que voleu calcular el pes d’un balancí amb una massa de 30 quilos. Com que és un objecte simètric, el seu centre de gravetat estarà exactament al centre (quan ningú no hi assegui). Però quan la gent de diferents masses es troba en el balancí, el problema es complica una mica.
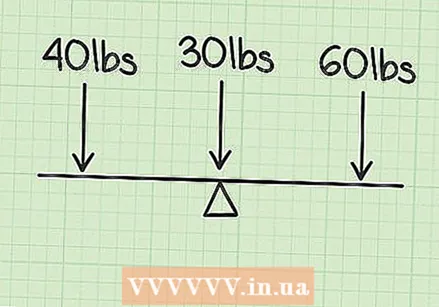2. Calculeu els pesos addicionals. Per determinar el centre de gravetat del balancí amb dos nens a sobre, haureu de determinar el pes individual de cada nen. El primer fill té una massa de 40 quilos i el segon, de 60 quilos.

Mètode 2 de 4: determineu el punt zero

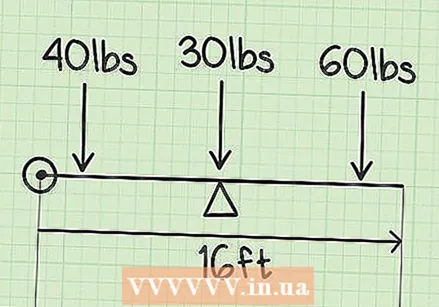1. Trieu un punt zero. El punt zero és qualsevol punt de partida d’un costat del balancí. Podeu col·locar el punt zero a un costat del balancí o a l’altre. Diguem que el balancí fa 6 metres de llarg. Posem el punt zero al costat esquerre del balancí, a prop del primer fill.
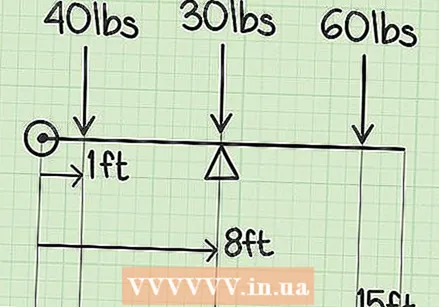2. Mesureu la distància des del punt zero fins al centre de l'objecte principal, així com fins als dos pesos addicionals. Suposem que els nens es troben cada 1 metre de cada extrem del balancí. El centre del balancí és el centre del balancí, o 3 metres, perquè 6 metres dividits per 2 equivalen a 3. A continuació, es mostren les distàncies del centre de l'objecte més gran i els dos pesos addicionals que formen el punt zero:
   • Centre del balancí = 4 metres del punt zero.
   • Nen 1 = 1 metre del punt zero
   • Nen 2 = a 5 metres del punt zero

Mètode 3 de 4: determinar el centre de gravetat

1. Multipliqueu la distància de cada objecte al punt zero pel seu pes per trobar el moment. Això us dóna el moment de cada objecte. A continuació s’explica com es multiplica la distància de cada objecte al punt zero pel seu pes:
   • El balancí: 30 kg x 3 m = 90 m * kg.
   • Nen 1 = 40 kg x 1 m = 40 m * kg.
   • Nen 2 = 60 kg x 5 m = 300 m * kg.
2. Afegiu els tres moments junts. Simplement calculeu el següent: 90 m * kg + 40 m * kg + 300 m * kg = 430 m * kg. El moment total és de 430 m * kg.
3. Sumeu els pesos de tots els objectes. Determineu la suma dels pesos del balancí i dels dos fills. Feu-ho de la següent manera: 30 quilos + 40 quilos + 60 quilos = 130 quilos.
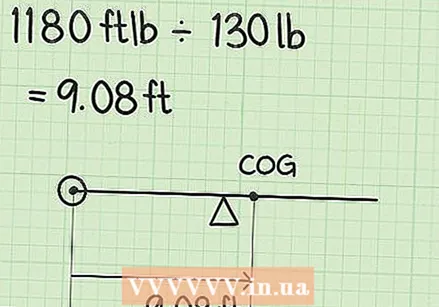4. Dividiu el moment total pel pes total. Això us donarà la distància des del punt zero fins al centre de gravetat de l’objecte. Això es divideix per 430 m * kg per 130 lliures.
   • 430 m * kg ÷ 130 quilos = 3,31 m
   • El centre de gravetat es troba a 3,31 metres del punt zero, o mesurat des del punt zero, es troba a 3,31 metres del final del costat esquerre del balancí on es va col·locar el punt zero.

Mètode 4 de 4: comproveu la vostra resposta

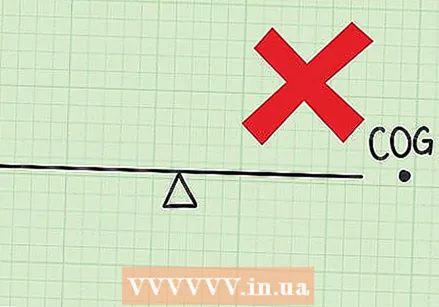1. Cerqueu el centre de gravetat al diagrama. Si el centre de gravetat que heu trobat està fora del sistema d’objectes, heu trobat la resposta equivocada. És possible que hàgiu calculat la distància de més d’un punt. Torneu-ho a provar amb només un punt zero.
   • Per exemple: per a les persones assegudes al balancí, el centre de gravetat ha d’estar en algun lloc del balancí, no a l’esquerra ni a la dreta del balancí. No ha de ser una persona.
   • Això també s'aplica a problemes en dues dimensions. Dibuixa un quadrat prou gran per adaptar-se a tots els objectes del problema. El centre de gravetat ha d’estar dins d’aquest quadrat.
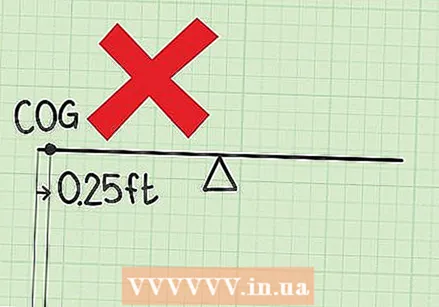2. Comproveu els càlculs si la resposta és massa petita. Si trieu un extrem del sistema com a punt zero, una petita resposta col·loca el centre de gravetat just al costat d’un extrem. Aquesta pot ser la resposta correcta, però sovint indica que alguna cosa ha fallat. Teniu el pes i la distància entre vosaltres en el càlcul multiplicat? Aquesta és la manera correcta de trobar aquest moment. Si accidentalment sumats, probablement obtindreu una resposta molt menor.
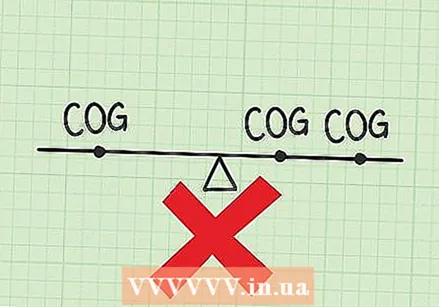3. Comproveu el càlcul si heu trobat més d’un centre de gravetat. Cada sistema només té un únic centre de gravetat. Si n'hi ha més, és possible que hàgiu saltat el pas en què havíeu d'afegir tots els moments junts. És el centre de gravetat total moment dividit pel total pes. Vostè no ha de cadascun moment per dividir per cadascun de pes, que només us proporciona la posició de cada objecte.
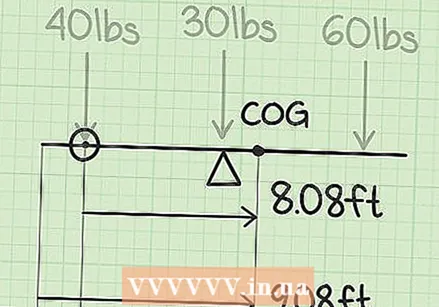4. Comproveu el punt zero si la resposta és un nombre enter al costat. La resposta del nostre exemple és de 3,31 m. Suposem que se us va donar 2,31 m, 4,31 m o algun altre número que acabi en ".31". Això és probablement perquè tenim l'extrem esquerre del balancí. Com a punt zero, mentre escolliu l'extrem dret o un altre punt a una distància d'un enter del nostre punt zero. La vostra resposta és correcta, independentment del punt zero que trieu. Només cal recordar-ho el punt zero sempre significa x = 0. Aquí teniu un exemple:
   • Com ho hem resolt, el punt zero es troba a la part esquerra del balancí. La nostra resposta és de 3,31 m, de manera que el nostre centre de massa es troba a 3,31 m del punt zero de l’esquerra.
   • Si escolliu un nou punt zero, trieu 1 m a l'esquerra, obtindreu 2,31 m del centre de massa com a resposta. El centre de massa és de 2,31 m des del nou punt zero, o a 1 m de l'esquerra. El centre de massa és de 2,31 + 1 = 3,31 m per l'esquerra, i amb això la mateixa resposta que hem calculat anteriorment.
   • (Nota: quan mesureu distància, recordeu distàncies a l'esquerra des del punt zero són negatius i les distàncies dret positiu.)
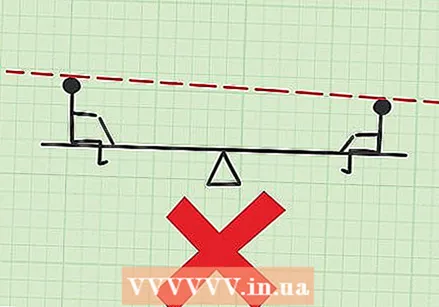5. Assegureu-vos que totes les vostres mesures siguin rectes. Suposem que veieu un altre exemple amb "nens en un balancí", però un nen és molt més alt que l'altre, o un noi penja sota el balancí en lloc de seure-hi. No feu cas a la diferència i feu totes les mesures al llarg de la línia recta del balancí. Mesurar distàncies en un racó donarà respostes properes, però lleugerament diferents.
   • Per als exercicis de balancí, l’important és que el centre de gravetat estigui d’esquerra a dreta al llarg de la línia del balancí. Més endavant, podeu aprendre formes més avançades de calcular el centre de gravetat en dues dimensions.

Consells

• Per determinar la distància a la qual s’ha de moure una persona per equilibrar el balancí del suport, utilitzeu aquesta fórmula: (pes desplaçat) / (pes total)=(distància sobre la qual s'ha mogut el centre de gravetat) / (distància sobre la qual s'ha mogut el pes ). Aquesta fórmula es pot reescriure per mostrar que la distància que s’ha de moure el pes (persona) és igual a la distància entre el centre de gravetat i el punt de suport multiplicat pel pes de la persona dividit pel pes total. Per tant, deu ser el primer fill -1,31 m * 40 quilos / 130 quilos =-0,40 m de desplaçament (fins al final del balancí). O hauria de girar el segon fill -1,08 m * 130 quilos / 60 quilos =Desplaçament -2,84 m. (cap al centre del balancí).
• Per trobar el centre de gravetat d’un objecte bidimensional, utilitzeu la fórmula Xcg = ∑xW / ∑W per trobar el centre de gravetat al llarg de l’eix x i Ycg = ∑yW / ∑W per trobar el centre de gravetat al llarg de la y eix a trobar. El punt en què es creuen és el centre de gravetat.
• La definició del centre de gravetat d’una distribució de massa general és (∫ r dW / ∫ dW) on dW és igual a la derivada del pes, r és el vector de posició i les integrals s’han d’interpretar com a integrals de Stieltjes sobre la tot el cos. Tot i així, es poden expressar com a integrals de volum de Riemann o Lebesgue més convencionals per a distribucions amb una funció de densitat de probabilitat. Començant per aquesta definició, totes les propietats CG, incloses les que s’utilitzen en aquest article, es poden derivar de les propietats integrals de Stieltjes.

Advertiments

• No intenteu aplicar cegament aquestes mecàniques sense entendre la teoria, que pot provocar errors. Primer, intenteu entendre les lleis / teories subjacents.