Content

• Passos
• Part 1 de 3: proves de simplicitat
• Part 2 de 3: Com funcionen les proves de simplicitat
• Part 3 de 3: Utilització del teorema de la resta de la Xina
• Consells
• Què necessites

Els nombres primers són nombres que són divisibles només per ells mateixos i per 1. La resta de nombres s’anomenen nombres compostos. Hi ha moltes maneres de determinar si un nombre és primer i tots tenen els seus propis avantatges i desavantatges. D'una banda, alguns dels mètodes són molt precisos, però són força complexos si es tracta de grans quantitats. D’altra banda, hi ha maneres molt més ràpides, però poden provocar resultats incorrectes. L'elecció del mètode adequat depèn de la mida de les xifres amb les quals esteu treballant.

Passos

Part 1 de 3: proves de simplicitat

Nota: en totes les fórmules n indica el número que s'ha de comprovar.

1. 1 Enumeració de divisors. N’hi ha prou amb dividir n a tots els nombres primers del 2 al valor arrodonit (${ displaystyle { sqrt {n}}}$).
2. 2 Petit teorema de Fermat. Advertència: de vegades, la prova identificarà falsament els nombres compostos com a primers, fins i tot per a tots els valors de a.
   • Escollim un nombre enter atal que 2 ≤ a ≤ n - 1.
   • Si a (mod n) = a (mod n), el nombre és probablement primer. Si no es compleix la igualtat, el número n és compost.
   • Comproveu la igualtat donada per a diversos valors aper augmentar la probabilitat que el nombre que s'està provant sigui realment primer.
3. 3 Prova Miller-Rabin. Advertència: de vegades, encara que rarament, per a diversos valors de a, la prova identificarà falsament els nombres compostos com a primers.
   • Trobeu les quantitats s i d tals que ${ displaystyle n-1 = 2 ^ {s} * d}$.
   • Seleccioneu un nombre enter a en el rang 2 ≤ a ≤ n - 1.
   • Si a = +1 (mod n) o -1 (mod n), llavors n és probablement primer. En aquest cas, aneu al resultat de la prova. Si la igualtat no es manté, aneu al següent pas.
   • Quadra la teva resposta (${ displaystyle a ^ {2d}}$). Si obteniu -1 (mod n), llavors n és probablement un nombre primer. En aquest cas, aneu al resultat de la prova. Si la igualtat falla, repetiu (${ displaystyle a ^ {4d}}$ i així successivament) fins ${ displaystyle a ^ {2 ^ {s-1} d}}$.
   • Si en algun pas després de quadrar un número diferent de ${ displaystyle pm 1}$ (mod n), teniu +1 (mod n), de manera que n és un nombre compost. Si ${ displaystyle a ^ {2 ^ {s-1} d} neq pm 1}$ (mod n), llavors n no és primer.
   • Resultat de la prova: si n supera la prova, repetiu-la per altres valors aper augmentar la confiança.

Part 2 de 3: Com funcionen les proves de simplicitat

1. 1 Enumeració de divisors. Per definició, el nombre n és simple només si no és divisible per 2 i altres enters excepte 1 i ell mateix. La fórmula anterior us permet eliminar passos innecessaris i estalviar temps: per exemple, després de comprovar si un nombre és divisible per 3, no cal comprovar si és divisible per 9.
   • La funció floor (x) arrodoneix x fins a l’enter més proper menor o igual a x.
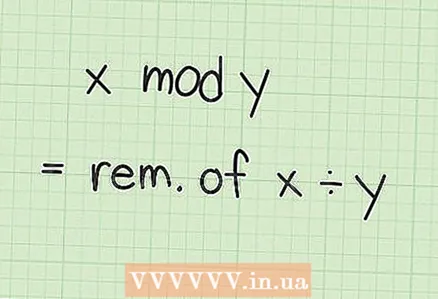2. 2 Més informació sobre l’aritmètica modular. L'operació "x mod y" (mod és una abreviatura de la paraula llatina "modulo", és a dir, "mòdul") significa "divideix x per y i troba la resta". Dit d’una altra manera, en aritmètica modular, en arribar a un determinat valor, que s’anomena mòdul, els números "tornen" a zero. Per exemple, el rellotge compta enrere amb el mòdul 12: mostra 10, 11 i 12 hores i després torna a 1.
   • Moltes calculadores tenen una tecla mod. Al final d'aquesta secció es mostra com es calcula manualment aquesta funció per a grans quantitats.
3. 3 Conegueu les trampes del Petit Teorema de Fermat. Tots els números per als quals no es compleixen les condicions de prova són compostos, però la resta de números només ho són probablement són simples. Si voleu evitar resultats incorrectes, cerqueu n a la llista de "nombres de Carmichael" (nombres compostos que compleixen aquesta prova) i "nombres de pseudoprime de Fermat" (aquests nombres compleixen les condicions de la prova només per a alguns valors a).
4. 4 Si és convenient, utilitzeu la prova Miller-Rabin. Tot i que aquest mètode és bastant pesat per als càlculs manuals, s’utilitza sovint en programes d’ordinador. Proporciona una velocitat acceptable i menys errors que el mètode de Fermat. Un número compost no es prendrà com a nombre primer si es fan càlculs per a més de ¼ valors a... Si escolliu diferents valors a l’atzar a i per a tots ells la prova donarà un resultat positiu, podem suposar amb un grau de confiança bastant alt que n és un nombre primer.
5. 5 Per a grans quantitats, utilitzeu aritmètica modular. Si no teniu a mà una calculadora de modificacions o la calculadora no està dissenyada per manejar un nombre tan gran, utilitzeu propietats de potència i aritmètica modular per facilitar els càlculs. A continuació es mostra un exemple per a ${ displaystyle 3 ^ {50}}$ mod 50:
   • Torneu a escriure l'expressió d'una forma més convenient: ${ displaystyle (3 ^ {25} * 3 ^ {25})}$ mod 50. Els càlculs manuals poden requerir més simplificacions.
   • ${ displaystyle (3 ^ {25} * 3 ^ {25})}$ mod 50 = ${ displaystyle (3 ^ {25}}$ mod 50 ${ displaystyle * 3 ^ {25}}$ mod 50) mod 50. Aquí es va tenir en compte la propietat de la multiplicació modular.
   • ${ displaystyle 3 ^ {25}}$ mod 50 = 43.
   • ${ displaystyle (3 ^ {25}}$ mod 50 ${ displaystyle * 3 ^ {25}}$ mod 50) mod 50 = ${ displaystyle (43 * 43)}$ mod 50.
   • ${ displaystyle = 1849}$ mod 50.
   • ${ displaystyle = 49}$.

Part 3 de 3: Utilització del teorema de la resta de la Xina

1. 1 Tria dos números. Un dels números ha de ser compost i l’altre ha de ser exactament el que voleu provar per simplicitat.
   • Nombre1 = 35
   • Nombre2 = 97
2. 2 Seleccioneu dos valors superiors a zero i, respectivament, inferiors als números Number1 i Number2. Aquests valors no han de ser els mateixos.
   • Valor1 = 1
   • Valor2 = 2
3. 3 Calculeu el MMI (invers matemàtic multiplicatiu) per al número 1 i al número 2.
   • Calculeu MMI
     • MMI1 = Number2 ^ -1 Mod Number1
     • MMI2 = Number1 ^ -1 Mod Number2
   • Només per a nombres primers (donarà un número per a nombres compostos, però no serà el seu MMI):
     • MMI1 = (Nombre2 ^ (Número1-2))% Nombre1
     • MMI2 = (Nombre1 ^ (Número2-2))% Nombre2
   • Per exemple:
     • MMI1 = (97 ^ 33)% 35
     • MMI2 = (35 ^ 95)% 97
4. 4 Creeu una taula per a cada MMI a mòduls log2:
   • Per a MMI1
     • F (1) = Nombre2% Nombre1 = 97% 35 = 27
     • F (2) = F (1) * F (1)% Nombre1 = 27 * 27% 35 = 29
     • F (4) = F (2) * F (2)% Nombre1 = 29 * 29% 35 = 1
     • F (8) = F (4) * F (4)% Nombre1 = 1 * 1% 35 = 1
     • F (16) = F (8) * F (8)% Nombre1 = 1 * 1% 35 = 1
     • F (32) = F (16) * F (16)% Nombre1 = 1 * 1% 35 = 1
   • Calculeu els números aparellats 1 - 2
     • 35 -2 = 33 (10001) base 2
     • MMI1 = F (33) = F (32) * F (1) mod 35
     • MMI1 = F (33) = 1 * 27 mod 35
     • MMI1 = 27
   • Per a MMI2
     • F (1) = Nombre1% Nombre2 = 35% 97 = 35
     • F (2) = F (1) * F (1)% Nombre2 = 35 * 35 mod 97 = 61
     • F (4) = F (2) * F (2)% Nombre2 = 61 * 61 mod 97 = 35
     • F (8) = F (4) * F (4)% Nombre2 = 35 * 35 mod 97 = 61
     • F (16) = F (8) * F (8)% Nombre2 = 61 * 61 mod 97 = 35
     • F (32) = F (16) * F (16)% Nombre2 = 35 * 35 mod 97 = 61
     • F (64) = F (32) * F (32)% Nombre2 = 61 * 61 mod 97 = 35
     • F (128) = F (64) * F (64)% Nombre2 = 35 * 35 mod 97 = 61
   • Calculeu el número emparellat 2 - 2
     • 97 - 2 = 95 = (1011111) base 2
     • MMI2 = (((((((F (64) * F (16)% 97) * F (8)% 97) * F (4)% 97) * F (2)% 97) * F (1)% 97)
     • MMI2 = ((((((35 * 35)% 97) * 61)% 97) * 35% 97) * 61% 97) * 35% 97)
     • MMI2 = 61
5. 5 Calcula (Valor1 * Número2 * MMI1 + Valor2 * Nombre1 * MMI2)% (Nombre1 * Número2)
   • Resposta = (1 * 97 * 27 + 2 * 35 * 61)% (97 * 35)
   • Resposta = (2619 + 4270)% 3395
   • Resposta = 99
6. 6 Comproveu que el número 1 no sigui primer
   • Calcula (Resposta - Valor1)% Nombre1
   • 99 – 1 % 35 = 28
   • Com que 28 és superior a 0, 35 no és un nombre primer.
7. 7 Comproveu que el número 2 sigui primer.
   • Calcula (Resposta - Valor2)% Nombre2
   • 99 – 2 % 97 = 0
   • Com que 0 és 0, 97 és probablement un nombre primer.
8. 8 Repetiu els passos del 1 al 7 almenys dues vegades més.
   • Si obteniu 0 al pas 7:
     • Utilitzeu un número1 diferent si el número1 no és primer.
     • Utilitzeu un altre número 1 si el número 1 és primer. En aquest cas, hauríeu d'obtenir 0 als passos 6 i 7.
     • Utilitzeu Significat1 i Significat2 diferents.
   • Si al pas 7 obteniu constantment 0, és probable que el número 2 sigui primer.
   • Els passos 1 a 7 poden provocar un error si el número 1 no és primer i el número 2 és divisor del número 1. El mètode descrit funciona en tots els casos quan els dos nombres són primers.
   • El motiu pel qual heu de repetir els passos de l'1 al 7 és perquè, en alguns casos, fins i tot si el número 1 i el número 2 no són primers, al pas 7 obtindreu 0 (per a un o ambdós números). Això poques vegades passa.Trieu un altre número1 (compost) i, si el número2 no és primer, llavors el número2 no serà igual al zero al pas 7 (excepte el cas en què el número 1 és divisor del número2; aquí els nombres primers sempre seran zero al pas 7).

Consells

• Nombres primers del 168 al 1000: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79 , 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211 , 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359 , 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509 , 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673 , 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853 , 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997.
• Tot i que la prova de força bruta és una prova tediosa quan es treballa amb grans quantitats, és força eficient per a petites quantitats. Fins i tot en el cas de nombres grans, comenceu per provar petits divisors i, a continuació, passeu a mètodes més sofisticats per comprovar la simplicitat dels nombres (si no es troben petits divisors).

Què necessites

• Paper, bolígraf o ordinador