Content

• Per trepitjar
• Part 1 de 4: Elaboració de la matriu
• Part 2 de 4: Aprenentatge de les operacions per resoldre un sistema amb una matriu
• Part 3 de 4: Combineu els passos per resoldre la galàxia
• Part 4 de 4: Comprovació de la solució
• Consells

Una matriu és una manera molt útil de representar nombres en un format de bloc, que després podeu utilitzar per resoldre un sistema d’equacions lineals. Si només teniu dues variables, és probable que utilitzeu un mètode diferent. Llegiu-ne a Resolució d’un sistema d’equacions per obtenir exemples d’aquests altres mètodes. Però si teniu tres o més variables, és ideal una matriu. Utilitzant combinacions repetides de multiplicació i suma, podeu arribar sistemàticament a una solució.

Per trepitjar

Part 1 de 4: Elaboració de la matriu

1. Verifiqueu que teniu prou dades. Per obtenir una solució única per a cada variable d’un sistema lineal que utilitza una matriu, heu de tenir tantes equacions com el nombre de variables que intenteu resoldre. Per exemple: amb les variables x, y i z necessiteu tres equacions. Si teniu quatre variables, necessiteu quatre equacions.
   • Si teniu menys equacions que el nombre de variables, descobrireu alguns límits de les variables (com x = 3y i y = 2z), però no podeu obtenir una solució precisa. Per a aquest article només treballarem cap a una solució única.
2. Escriviu les vostres equacions en el formulari estàndard. Abans de poder posar les dades de les equacions en una forma matricial, primer escriviu cada equació en forma estàndard. La forma estàndard per a una equació lineal és Ax + By + Cz = D, on les lletres majúscules són els coeficients (números) i l’últim número (D en aquest exemple) es troba a la dreta del signe igual.
   • Si teniu més variables, continueu la línia el temps que necessiteu. Per exemple, si intentéssiu resoldre un sistema amb sis variables, la vostra forma predeterminada semblaria Au + Bv + Cw + Dx + Ey + Fz = G. En aquest article ens centrarem en sistemes amb només tres variables. Resoldre una galàxia més gran és exactament el mateix, però només necessita més temps i més passos.
   • Tingueu en compte que, de forma estàndard, les operacions entre els termes sempre són una suma. Si hi ha una resta a la vostra equació, en lloc d'una suma, haureu de treballar més endavant fent que el vostre coeficient sigui negatiu. Per fer-ho més fàcil de recordar, podeu reescriure l’equació i afegir l’operació i fer que el coeficient sigui negatiu. Per exemple, podeu reescriure l'equació 3x-2y + 4z = 1 com a 3x + (- 2y) + 4z = 1.
3. Col·loqueu els números del sistema d’equacions en una matriu. Una matriu és un grup de nombres, disposats en una mena de taula, amb la qual treballarem per resoldre el sistema. Bàsicament conté les mateixes dades que les pròpies equacions, però en un format més senzill. Per fer la matriu de les vostres equacions en forma estàndard, només cal que copieu els coeficients i el resultat de cada equació en una sola fila i apileu-les una sobre l'altra.
   • Suposem que teniu un sistema format per les tres equacions 3x + y-z = 9, 2x-2y + z = -3 i x + y + z = 7. La fila superior de la vostra matriu contindrà els números 3, 1, -1, 9, ja que aquests són els coeficients i la solució de la primera equació. Tingueu en compte que qualsevol variable que no tingui un coeficient se suposa que té un coeficient d'1. La segona fila de la matriu esdevé 2, -2, 1, -3 i la tercera fila es converteix en 1, 1, 1, 7.
   • Assegureu-vos d’alinear els coeficients x a la primera columna, els coeficients y a la segona, els coeficients z a la tercera i els termes de la solució a la quarta. Quan hàgiu acabat de treballar amb la matriu, aquestes columnes seran importants a l’hora d’escriure la vostra solució.
4. Dibuixeu un claudàtor gran al voltant de tota la vostra matriu. Per convenció, una matriu s’indica amb un parell de claudàtors, [], al voltant de tot el bloc de nombres. Els claudàtors no afecten la solució de cap manera, però indiquen que esteu treballant amb matrius. Una matriu pot consistir en qualsevol nombre de files i columnes. En aquest article, utilitzarem parèntesis al voltant de termes seguits per indicar que pertanyen junts.
5. Ús del simbolisme comú. Quan es treballa amb matrius, és habitual referir-se a les files amb l’abreviatura R i a les columnes amb l’abreviatura C. Podeu utilitzar números junt amb aquestes lletres per indicar una fila o columna específica. Per exemple, per indicar la fila 1 d'una matriu, podeu escriure R1. La fila 2 esdevé llavors R2.
   • Podeu indicar qualsevol posició específica en una matriu mitjançant una combinació de R i C. Per exemple, per indicar un terme a la segona fila, tercera columna, podeu anomenar-lo R2C3.

Part 2 de 4: Aprenentatge de les operacions per resoldre un sistema amb una matriu

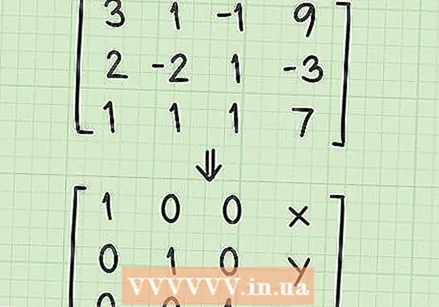1. Comprendre la forma de la matriu de la solució. Abans de començar a resoldre el vostre sistema d’equacions, heu d’entendre què fareu amb la matriu. En aquest moment teniu una matriu que té aquest aspecte:
   • 3 1 -1 9
   • 2 -2 1 -3
   • 1 1 1 7
   • Treballeu amb diverses operacions bàsiques per crear la "matriu de solucions". La matriu de la solució serà així:
   • 1 0 0 x
   • 0 1 0 anys
   • 0 0 1 z
   • Tingueu en compte que la matriu consisteix en 1 en una línia diagonal amb 0 en tots els altres espais excepte la quarta columna. Els números de la quarta columna són la solució de les variables x, y i z.
2. Utilitzeu la multiplicació escalar. La primera eina a la vostra disposició per resoldre un sistema mitjançant una matriu és la multiplicació escalar. Això és simplement un terme que significa que multiplica els elements d'una fila de la matriu per un nombre constant (no una variable). Quan utilitzeu la multiplicació escalar, tingueu en compte que heu de multiplicar cada terme de tota la fila pel nombre que seleccioneu. Si oblideu el primer terme i us multipliqueu, obtindreu la solució equivocada. Tot i això, no cal que multipliqueu tota la matriu al mateix temps. En la multiplicació escalar, només es treballa en una fila a la vegada.
   • És freqüent utilitzar fraccions en la multiplicació escalar perquè sovint es vol obtenir una fila diagonal de 1. Acostuma’t a treballar amb fraccions. També serà més fàcil (durant la majoria dels passos per resoldre la matriu) poder escriure les vostres fraccions de forma incorrecta i convertir-les de nou en nombres mixtos per a la solució final. Per tant, el número 1 2/3 és més fàcil de treballar si l’escriviu com a 5/3.
   • Per exemple, la primera fila (R1) del nostre exemple de problema comença amb els termes [3,1, -1,9]. La matriu de la solució ha de contenir un 1 a la primera posició de la primera fila. Per "canviar" el 3 per un 1, podem multiplicar la fila sencera per 1/3. Això crea el nou R1 de [1,1 / 3, -1 / 3,3].
   • Assegureu-vos de deixar els signes negatius on pertanyin.
3. Utilitzeu la suma de files o la resta de files. La segona eina que podeu utilitzar és afegir o restar dues files de la matriu. Per crear els termes 0 a la matriu de la solució, heu de sumar o restar números per arribar al 0. Per exemple, si R1 és d'una matriu [1,4,3,2] i R2 és [1,3,5,8], podeu restar la primera fila de la segona fila i crear-ne una nova [0, -1, 2,6], perquè 1-1 = 0 (primera columna), 3-4 = -1 (segona columna), 5-3 = 2 (tercera columna) i 8-2 = 6 (quarta columna). Quan realitzeu una suma o resta de files, torneu a escriure el resultat nou en lloc de la fila amb què heu començat. En aquest cas, trauríem la fila 2 i inseriríem la nova fila [0, -1,2,6].
   • Podeu utilitzar una notació abreujada i declarar aquesta acció com a R2-R1 = [0, -1,2,6].
   • Recordeu que la suma i la resta són formes just oposades de la mateixa operació. Penseu en això com sumant dos nombres o restant el contrari. Per exemple, si comenceu amb l'equació simple 3-3 = 0, podeu pensar en això com un problema d'addició de 3 + (- 3) = 0. El resultat és el mateix. Sembla senzill, però de vegades és més fàcil considerar un problema d’una forma o d’una altra. Només cal vigilar els signes negatius.
4. Combineu l'addició de files i la multiplicació escalar en un sol pas. No podeu esperar que els termes coincideixin sempre, de manera que podeu utilitzar una simple suma o resta per crear 0 a la vostra matriu. Més sovint haureu d'afegir (o restar) un múltiple d'una altra fila. Per fer-ho, primer feu la multiplicació escalar i, a continuació, afegiu aquest resultat a la fila de destinació que esteu intentant canviar.
   • Suposem; que hi ha una fila 1 de [1,1,2,6] i una fila 2 de [2,3,1,1]. Voleu un terme 0 a la primera columna de R2. És a dir, voleu canviar el 2 a un 0. Per fer-ho, heu de restar un 2. Podeu obtenir un 2 multiplicant primer la fila 1 per la multiplicació escalar 2 i restant la primera fila de la segona fila. En resum, es pot anotar com a R2-2 * R1. En primer lloc, multipliqueu R1 per 2 per obtenir [2,2,4,12]. A continuació, resteu això de R2 per obtenir [(2-2), (3-2), (1-4), (1-12)]. Simplifiqueu això i el vostre nou R2 serà [0,1, -3, -11].
5. Copieu les files que es mantinguin sense canvis mentre treballeu. Mentre treballeu a la matriu, canvieu una sola fila a la vegada, ja sigui mitjançant la multiplicació escalar, la suma de files o la resta de files o una combinació de passos. Quan canvieu una fila, assegureu-vos de copiar les altres files de la matriu en la forma original.
   • Es produeix un error comú en realitzar un pas combinat de multiplicació i suma en un sol moviment. Per exemple, suposem que cal restar R1 de R2 dues vegades. Quan multipliqueu R1 per 2 per fer aquest pas, recordeu que R1 no canvia a la matriu. Només feu la multiplicació per canviar R2. Primer copieu R1 en la seva forma original i, a continuació, feu el canvi a R2.
6. Primer treball de dalt a baix. Per resoldre el sistema, es treballa en un patró molt organitzat, essencialment "resolent" un terme de la matriu a la vegada. La seqüència d'una matriu de tres variables serà la següent:
   • 1. Feu un 1 a la primera fila, primera columna (R1C1).
   • 2. Feu un 0 a la segona fila, primera columna (R2C1).
   • 3. Feu un 1 a la segona fila, segona columna (R2C2).
   • 4. Feu un 0 a la tercera fila, primera columna (R3C1).
   • 5. Feu un 0 a la tercera fila, segona columna (R3C2).
   • 6. Feu un 1 a la tercera fila, tercera columna (R3C3).
7. Torneu a treballar de baix a dalt. En aquest punt, si heu fet els passos correctament, esteu a la meitat de la solució. Heu de tenir la línia diagonal d'1, amb 0 a sota. Els números de la quarta columna no importen en aquest moment. Ara torneu a la part superior de la manera següent:
   • Creeu un 0 a la segona fila, tercera columna (R2C3).
   • Creeu un 0 a la primera fila, tercera columna (R1C3).
   • Creeu un 0 a la primera fila, a la segona columna (R1C2).
8. Comproveu si heu creat la matriu de la solució. Si el vostre treball és correcte, heu creat la matriu de la solució amb 1 en una línia diagonal de R1C1, R2C2, R3C3 i 0 en les altres posicions de les tres primeres columnes. Els números de la quarta columna són les solucions per al vostre sistema lineal.

Part 3 de 4: Combineu els passos per resoldre la galàxia

1. Comenceu amb un sistema d'exemple d'equacions lineals. Per practicar aquests passos, comencem pel sistema que hem utilitzat anteriorment: 3x + y-z = 9, 2x-2y + z = -3 i x + y + z = 7. Si ho escriviu en una matriu, teniu R1 = [3,1, -1,9], R2 = [2, -2,1, -3] i R3 = [1,1,1,7].
2. Creeu un 1 a la primera posició R1C1. Tingueu en compte que R1 comença amb un 3. En aquest moment, heu de canviar-lo per 1. Podeu fer-ho mitjançant la multiplicació escalar, multiplicant els quatre termes de R1 per 1/3. En resum, podeu escriure com a R1 * 1/3. Això dóna un nou resultat per R1 si R1 = [1,1 / 3, -1 / 3,3]. Copieu R2 i R2, sense canvis, quan R2 = [2, -2,1, -3] i R3 = [1,1,1,7].
   • Tingueu en compte que la multiplicació i la divisió només són funcions inverses. Podem dir que multiplicem per 1/3 o dividim per 3, sense canviar el resultat.
3. Creeu un 0 a la segona fila, primera columna (R2C1). En aquest moment, R2 = [2, -2,1, -3]. Per acostar-vos a la matriu de la solució, heu de canviar el primer terme de 2 a 0. Podeu fer-ho restant el doble del valor de R1, ja que R1 comença per un 1. En resum, l’operació R2-2 * R1. Recordeu que no canvieu R1, només heu de treballar-hi. Per tant, primer copieu R1 si R1 = [1,1 / 3, -1 / 3,3]. Aleshores, si dupliqueu cada terme de R1, obtindreu 2 * R1 = [2,2 / 3, -2 / 3,6]. Finalment, resteu aquest resultat del R2 original per obtenir el vostre nou R2. Treballant terme per terme, aquesta resta es converteix en (2-2), (-2-2 / 3), (1 - (- 2/3)), (-3-6). Els simplifiquem al nou R2 = [0, -8 / 3,5 / 3, -9]. Tingueu en compte que el primer terme és 0 (sigui quin sigui el vostre objectiu).
   • Escriviu la fila 3 (que no ha canviat) com a R3 = [1,1,1,7].
   • Aneu amb compte a l'hora de restar números negatius per assegurar-vos que els signes siguin correctes.
   • Ara primer deixem les fraccions en la forma incorrecta. Això facilita els passos posteriors de la solució. Podeu simplificar les fraccions a l'últim pas del problema.
4. Creeu un 1 a la segona fila, segona columna (R2C2). Per continuar formant la línia diagonal de 1, heu de convertir el segon terme -8/3 en 1. Feu-ho multiplicant tota la fila pel recíproc d'aquest nombre (-3/8). Simbòlicament, aquest pas és R2 * (- 3/8). La segona fila resultant és R2 = [0,1, -5 / 8,27 / 8].
   • Tingueu en compte que si la meitat esquerra de la fila comença a assemblar-se a la solució amb el 0 i l’1, la meitat dreta pot començar a semblar lletja, amb fraccions inadequades. Deixeu-los pel que són ara per ara.
   • No oblideu continuar copiant les files intactes, de manera que R1 = [1,1 / 3, -1 / 3,3] i R3 = [1,1,1,7].
5. Creeu un 0 a la tercera fila, primera columna (R3C1). El vostre enfocament es mou ara a la tercera fila, R3 = [1,1,1,7]. Per fer un 0 a la primera posició, heu de restar un 1 de l'1 que hi ha actualment en aquesta posició. Si mireu cap amunt, hi ha un 1 a la primera posició de R1. Per tant, només cal restar R1 de R3 per obtenir el resultat que necessiteu. Termini de treball per terme, es converteix en (1-1), (1-1 / 3), (1 - (- 1/3)), (7-3). Aquests quatre mini-problemes es poden simplificar al nou R3 = [0,2 / 3,4 / 3,4].
   • Continueu copiant al llarg de R1 = [1,1 / 3, -1 / 3,3] i R2 = [0,1, -5 / 8,27 / 8]. Recordeu que només canvieu una fila a la vegada.
6. Feu un 0 a la tercera fila, segona columna (R3C2). Actualment, aquest valor és 2/3, però s’ha de convertir a 0. A primera vista, sembla que podeu restar els valors R1 per doble, ja que la columna corresponent de R1 conté un 1/3. Tanmateix, si dupliqueu i resteu tots els valors de R1, el 0 de la primera columna de R3 canvia, cosa que no voleu. Aquest seria un pas enrere en la vostra solució. Per tant, heu de treballar amb alguna combinació de R2. Restant 2/3 de R2 es crea un 0 a la segona columna, sense canviar la primera columna. En resum, és R3-2 / 3 * R2. Els termes individuals es converteixen en (0-0), (2 / 3-2 / 3), (4/3 - (- 5/3 * 2/3)), (4-27 / 8 * 2/3) . La simplificació dóna llavors R3 = [0,0,42 / 24,42 / 24].
7. Creeu un 1 a la tercera fila, tercera columna (R3C3). Es tracta d’una multiplicació simple pel recíproc del nombre que diu. El valor actual és 42/24, de manera que podeu multiplicar per 24/42 per obtenir el valor que voleu 1. Tingueu en compte que els dos primers termes són 0, de manera que qualsevol multiplicació continua sent 0. El nou valor de R3 = [0,0,1,1].
   • Tingueu en compte que les fraccions que semblaven bastant complicades en el pas anterior ja comencen a resoldre's.
   • Continueu amb R1 = [1,1 / 3, -1 / 3,3] i R2 = [0,1, -5 / 8,27 / 8].
   • Tingueu en compte que en aquest punt teniu la diagonal d'1 per a la matriu de la solució. Només heu de convertir tres elements de la matriu en 0 per trobar la vostra solució.
8. Creeu un 0 a la segona fila, tercera columna. R2 és actualment [0,1, -5 / 8,27 / 8], amb un valor de -5/8 a la tercera columna. L'haureu de transformar a 0. Això vol dir que heu de realitzar alguna operació amb R3 que consisteix a afegir 5/8. Com que la tercera columna corresponent de R3 és un 1, heu de multiplicar tots els valors de R3 per 5/8 i afegir el resultat a R2. En resum, això és R2 + 5/8 * R3. El terme per terme és R2 = (0 + 0), (1 + 0), (-5 / 8 + 5/8), (27/8 + 5/8). Això es pot simplificar a R2 = [0,1,0,4].
   • A continuació, copieu R1 = [1,1 / 3, -1 / 3,3] i R3 = [0,0,1,1].
9. Creeu un 0 a la primera fila, tercera columna (R1C3). Actualment, la primera fila és R1 = [1,1 / 3, -1 / 3,3]. Heu de convertir el -1/3 de la tercera columna a 0, fent servir alguna combinació de R3. No voleu utilitzar R2, perquè l'1 de la segona columna de R2 canviaria R1 de manera equivocada. De manera que multipliqueu R3 * 1/3 i afegiu el resultat a R1. La notació per a això és R1 + 1/3 * R3. El terme per a l'elaboració de termes resulta en R1 = (1 + 0), (1/3 + 0), (-1 / 3 + 1/3), (3 + 1/3). Podeu simplificar-ho amb un nou R1 = [1,1 / 3,0,10 / 3].
   • Copieu R2 = [0,1,0,4] i R3 = [0,0,1,1] sense canvis.
10. Feu un 0 a la primera fila, a la segona columna (R1C2). Si tot es fa correctament, aquest hauria de ser l’últim pas. Heu de convertir 1/3 de la segona columna a 0. Podeu obtenir-ho multiplicant i restant R2 * 1/3. Breument, es tracta de R1-1 / 3 * R2. El resultat és R1 = (1-0), (1 / 3-1 / 3), (0-0), (10 / 3-4 / 3). Simplificant donarà R1 = [1,0,0,2].
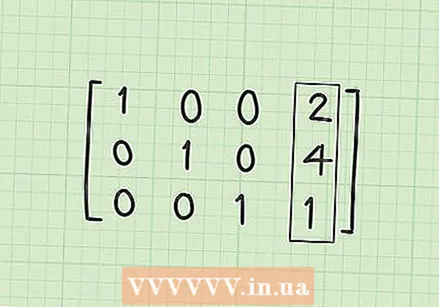11. Cerqueu la matriu de la solució. En aquest punt, si tot anés bé, tindríeu les tres files R1 = [1,0,0,2], R2 = [0,1,0,4] i R3 = [0,0,1,1] ha de tenir. Tingueu en compte que si escriviu això a la forma de matriu de blocs amb les files una sobre l'altra, teniu les diagonals 1 amb 0 més, i les vostres solucions es troben a la quarta columna. La matriu de la solució hauria de ser així:
    • 1 0 0 2
    • 0 1 0 4
    • 0 0 1 1
12. Comprendre la vostra solució. Després de convertir les equacions lineals en una matriu, poseu els coeficients x a la primera columna, els coeficients y a la segona columna i els coeficients z a la tercera columna. Si voleu tornar a escriure la matriu a equacions, aquestes tres línies de la matriu signifiquen les tres equacions 1x + 0y + 0z = 2, 0x + 1y + 0z = 4 i 0x + 0y + 1z = 1. Com que podem ratllar els 0 termes i no haver d’escriure els 1 coeficients, aquestes tres equacions es simplifiquen per a la solució, x = 2, y = 4 i z = 1. Aquesta és la solució al vostre sistema d’equacions lineals.

Part 4 de 4: Comprovació de la solució

1. Incloeu les solucions a cada variable de cada equació. Sempre és una bona idea comprovar que la vostra solució sigui realment correcta. Ho feu provant els vostres resultats en les equacions originals.
   • Les equacions originals d’aquest problema eren: 3x + y-z = 9, 2x-2y + z = -3 i x + y + z = 7. Quan substituïu les variables pels seus valors que heu trobat, obteniu 3 * 2 + 4-1 = 9, 2 * 2-2 * 4 + 1 = -3 i 2 + 4 + 1 = 7.
2. Simplifiqueu qualsevol comparació. Realitzeu les operacions de cada equació segons les regles bàsiques de les operacions. La primera equació es simplifica a 6 + 4-1 = 9 o 9 = 9. La segona equació es pot simplificar a 4-8 + 1 = -3 o -3 = -3. La darrera equació és simplement 7 = 7.
   • Com que qualsevol equació es simplifica en una afirmació matemàtica real, les vostres solucions són correctes. Si alguna de les solucions és incorrecta, reviseu el vostre treball i busqueu errors. Alguns errors comuns es produeixen en desfer-se dels signes menys al llarg del camí o confondre la multiplicació i l'addició de fraccions.
3. Escriu les teves solucions finals. Per a aquest problema donat, la solució final és x = 2, y = 4 i z = 1.

Consells

• Si el vostre sistema d'equacions és molt complex, amb moltes variables, és possible que pugueu utilitzar una calculadora gràfica en lloc de fer la feina a mà. Per obtenir informació sobre això, també podeu consultar wikiHow.